Мир, знаем мы, живой – он дышит.
Его дыханье – суть волна.
И представленья – выше – тише,
Быстрее – медленней – она –
Везде волна – закон дыханья.
Любовь и ненависть – контраст –
Есть амплитуда колебанья –
Вот кто-то вспыхнул и угас…
И взрыв Большой – всему начало –
Был чей-то выдох, буде вдох.
Всех на волне морской качало,
Все проходили тот урок,
Когда подбрасывало выше,
Бросало резко вниз потом.
И звук то громче был, то тише
И замирало все кругом,
Как будто кончилось пространство…
Но разгоралась вновь заря,
И было продолженье странствий,
И поднимались якоря.
А.С. Латкин
Научно-исследовательский геотехнологический центр ДВО РАН,
Северо-Восточное шоссе, 30, 683002, г. Петропавловск-Камчатский, Россия
Аннотация. На основании анализа решения математических моделей предлагается расчет структуры движения межпланетного вещества в планетарной системе и формулируется гипотеза, объясняющая продолжительность существования звездных систем во Вселенной.
Циркуляционное движение самое распространенное во Вселенной: фотографии Галактик, движение воды, обмен газов в биосфере, все обменные и жизненные процессы – вот неполный перечень доказательств этому. Вместе с тем, циркуляционные движения – одни из самых загадочных явлений в природе: закрученное движение газового или жидкостного потока создает поля центробежных сил, развитой турбулентной структуры и градиента температур, поток электронов в соленоиде формирует электромагнитное поле и, вполне возможно, что поток фотонов в соленоиде из световода рождает, в свою очередь, какое-то физическое поле.
Однако, если явления, связанные с наличием центробежного поля и пульсационного движения, можно довольно точно рассчитать, то для явлений, связанных с температурным разделением, формированием электромагнитных полей, существует только ряд спорных, не вполне обоснованных гипотез - ведь даже образование обычной воронки при истечении жидкости мы не в состоянии не то что рассчитать, но даже внятно объяснить.
Это происходит в результате сложности экспериментального исследования циркуляционных процессов и ограниченной возможности вести исследования аналитическими способами. Имеющиеся исследования циркуляционного движения проводились для зон малых размеров: от технологических вихревых устройств до природных «циклонов» (степень изученности которых не сопоставимо ниже вихревых устройств).
Из-за сложности решения уравнений движения (Эйлера, Навье-Стокса и Рейнольдса) в настоящее время имеются аналитические решения для двух видов вращательного движения: 1 - потенциальное вращение симметричного плоского потока; 2 - твердое вращение.
Несмотря на ограниченность применения, эти решения могут дать информацию для качественного анализа циркуляционного движения. В виде примера рассмотрим движение планет в звездных системах. Так как в настоящее время наиболее изученной является солнечная система, возьмем ее за образец, то есть будем считать, что у большинства звездных систем наблюдаются те же закономерности. Все планеты вращаются вокруг Солнца практически в одной плоскости, орбиты вращения близки к круговым, а орбитальные скорости в зависимости от расстояния от Солнца подчиняются квазипотенциальному закону из-за малого трения с межпланетной средой. Изложенные факты определяют граничные условия:
![]() >
>
![]() >
>
![]() ; Vj
>
Vr
>Vz,
(1)
; Vj
>
Vr
>Vz,
(1)
где r – расстояние от Солнца до точки в плоскости вращения планет и, соответственно, радиальная координата; j – угловая координата; z – координата перпендикулярная плоскости вращения планет; Vj ; Vr ; Vz - тангенциальная, радиальная и осевая составляющие векторы скорости движения системы.
Допустим, что такая закономерность характерна не только для движения планет солнечной системы, но и для большинства звезд, имеющих систему планет, вращающихся вокруг них. Поэтому в дальнейшем имеет смысл оперировать понятиями Звезда, планета, межзвездное и межпланетное вещество, а адекватность рассуждений оценивать имеющимися данными для Солнца и солнечной системы, так как для звезд они пока отсутствуют.
Допуская, что концентрация межпланетного вещества невелика по сравнению с массой системы, то трением можно пренебречь и для анализа за исходное взять уравнение Эйлера для стационарного движения, т.к. изменений в системе за время наблюдений не наблюдалось:
![]() =
=
![]() ,
(2)
,
(2)
где r – средняя плотность вещества; v – вектор скорости; l – пространственная координата; P – давление в системе.
Преобразуем векторное уравнение (2) в три скалерных и запишем их в цилиндрической системе координат с учетом граничных условий (1). В результате получим следующую систему уравнений:
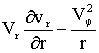 =
=
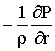 ;
;
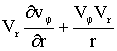 = 0;
(3)
= 0;
(3)
![]() = 0.
= 0.
Система дифференциальных уравнений (3) имеет аналитическое решение [1]:
Vr = C/r; Vj = C1/r; D P = C2 - r (C2 - C12) / 2r2, (4)
где D Р- перепад давления; С, С1, С2 - постоянные интегрирования.
Анализ полученного решения показывает, что в результате вращения системы имеется градиент давления межпланетного вещества в плоскости вращения планет, а в области звезды (центра вращения) давление межпланетного вещества ниже среднего давления в пространстве. Таким образом, создается возможность поступления вещества Вселенной, состоящего на 80-90% из водорода, к поверхности звезды. Учитывая интенсивность тепломассообменных явлений в этой зоне, подводимое вещество может явиться топливом для термоядерных процессов в ходе существования звездной системы.
Данная гипотеза позволяет объяснить длительное время существования солнечной системы, так как существование Солнца только за счет термоядерных процессов в массе его вещества возможно только 3-4 десятка тысяч лет. А самое главное – решается парадокс, который хорошо известен в астрономии: температура газа в солнечной короне значительно выше температуры поверхности Солнца. С позиций термоядерного процесса в объеме это совершенно непонятно, однако если термоядерные процессы идут за счет подводимого к звезде водорода из пространства, то все становится объяснимым – термоядерные процессы, связанные с синтезом легких элементов из водорода, идут в короне Солнца (и этот процесс, по всей видимости, характерен для любой звезды). В результате этого идет интенсивный подвод энергии к поверхности звезды, что дает возможность, при наличии различных продуктов термоядерного синтеза, формировать ее структуру за счет синтеза более тяжелых элементов в ее объеме, вплоть до трансурановых, с массами, намного большими известных нам.
Существуют факты прямого подтверждения справедливости данной гипотезы: во- первых, масса вещества, поступающего на звезду, значительна, так как опыт межпланетных полетов показал, что концентрация межпланетного вещества на 3-4 порядка выше, чем считалось ранее; во-вторых, тангенциальная составляющая, полученная в результате решения исходной системы (3), значительно выше реальных скоростей вращения планет, а это можно объяснить только высоким внутренним трением в результате движения вещества в солнечной системе.
Встает вопрос, а следует ли принимать к рассмотрению модели, которые дают такую ошибку, в то время когда решения, предложенные Ньютоном для солнечной системы, достаточно полно описывают реально движение планет. Рассмотрим решение Ньютона, полученное из баланса гравитационной силы, действующей между звездой и планетой (Fгр = gmM/R2), и центробежной силы, удерживающей планету на орбите (Fцб = mVj2/R). Из этих условий можно определить реальную скорость вращения планеты
Vj = C2 / r1/2. (5)
Уравнение Ньютона на основе баланса гравитационных и центробежных сил движения планет по их орбитам является кинематическим и не в состоянии объяснить причины движения системы. Модель на основе решения уравнения Эйлера может дать только основу для качественного анализа, который нам уже показал необходимость учета вязкости. Поэтому для качественной оценки динамического взаимодействия системы нам необходимо использовать уравнение Навье-Стокса. Тогда для исходных граничных условий получим:
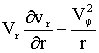 =
=
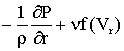 ;
;
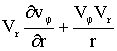 =
=
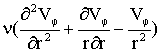 ;
(6)
;
(6)
![]() = 0.
= 0.
здесь n - коэффициент кинематической вязкости пространства.
Значение скорости движения вещества планетарной системы в радиальном направлении можно получить из решения третьего уравнения системы (6):
Vr = C/ri, (7)
где ri
– текущий
радиус в
планетарной
системе,
![]() –
гравитационная
постоянная, m
и M – массы
планеты и
звезды
соответственно,
R -
радиус
орбиты
планеты.
–
гравитационная
постоянная, m
и M – массы
планеты и
звезды
соответственно,
R -
радиус
орбиты
планеты.
Подставив уравнения (5) и (7) во второе уравнение системы (6), найдем распределение коэффициента кинематической вязкости n межпланетной среды и его изменение по радиусу планетарной системы:
n = 2C/ (2ri + 1). (8)
Анализ полученного соотношения показывает, что в пространстве около Звезды вязкость межзвездного вещества значительна, и, следовательно, наличие внутреннего трения приведет к изменению закона вращения межзвездного вещества от квазипотенциального Vj = C / f(r) к квазитвердому Vj = C f(r).
Общий профиль тангенциальной составляющей можно найти на основе следующих простейших рассуждений. Период движения вещества и планет в реальной звездной системе Т можно найти из уравнения:
T = D T + ri / C1, (9)
где ri / C1 - период вращения системы при потенциальном вращении, D T - приращение периода вращения из-за сил внутреннего трения. Тогда учитывая, что угловая скорость вращения – величина, обратная периоду вращения, а линейная равна произведению угловой скорости на радиус вращения, получим [2]:
Vj = Vjmax Ch / (1 + h2), (10)
где Vjmax - максимальное значение скорости вращения межпланетного вещества в орбитальной системе на радиусе Rjmax, h = ri / rjmax - новая переменная, являющаяся величиной безразмерного радиуса вращения системы.
Уравнение (10) носит частный характер, так как получено из общих рассуждений, и решение системы (6) на основании введения данной аппроксимации дает возможность определить закономерности движения материи в звездной системе со строго фиксированными параметрами, носящими только качественный характер. Эксперименты показывают наличие самых разнообразных вихревых структур [2], решения для которых можно найти из самого уравнения Навье-Стокса. Градиент давления вязкой несжимаемой жидкости по тангенциальной составляющей для вихревых аппаратов в цилиндрических координатах можно записать в виде:
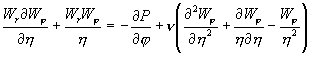 ,
(11)
,
(11)
где Wi =Vi / Vjmax - безразмерное текущее значение составляющей вектора скорости, Vi - текущее значение составляющей вектора скорости.
Так как в расчетах вращение потока принимается осесимметричным, то полученное уравнение можно преобразовать к виду:
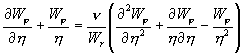 .
(12)
.
(12)
Отношение n/Wr, согласно экспериментальным данным [2], можно аппроксимировать уравнением n/Wr = Ch / (1 - h), так как величина n в любой точке вихревой камеры имеет положительное значение, а Wr меняет свое значение в окрестности h ~ 1.
Дифференциальное уравнение (12) с учетом аппроксимации n/Wr имеет два решения: Wj1 = C/h; Wj2 = C(h + 2 - 2/h)e-h. Анализ полученных уравнений [7] показал, что слагаемое Che-h cоответствует реальному профилю тангенциальной составляющей вектора скорости закрученного потока и является более универсальным для описания существующего диапазона вариаций режимно-конструктивных параметров циклонно-вихревых устройств, описываемых функциями типа:
![]() (13)
(13)
где m - показатель степени, зависящий от характеристик пространства формирования планетной системы.
Решение системы (6) уравнений (1) - (3) после подстановки в них выражения (13) позволяют определить уравнения радиальной и аксиальной составляющих вектора скорости и распределения давления во вращающейся системе [2,3]:
![]() = 2a2.(he1-h)m
. [(1+m-mh)2-
mh],
(14)
= 2a2.(he1-h)m
. [(1+m-mh)2-
mh],
(14)
![]() [(1+m-mh)3-3mh(1+m-
mh)-
mh]+С,
(15)
[(1+m-mh)3-3mh(1+m-
mh)-
mh]+С,
(15)
DP=
![]() (16)
(16)
Наличие вязкости межзвездного вещества позволяет предложить схему существования и развития звезды с планетарной системой (в том числе солнечной).
Движение межзвездного вещества при наличии вязкости на определенном участке Вселенной создает вихревые зоны подобно вихрям около газовых или жидкостных потоков. В результате создаются условия для поступления межзвездного вещества в центр вихревой зоны, где происходит его накопление под действием гравитационных сил. При достижении массы выше критического значения начинается процесс термоядерного синтеза, возникает звезда, а выброс лишней массы в пространство позволяет формировать планеты и их спутники. Наиболее вероятно, что дальнейшее развитие и существование звездной системы происходит под влиянием двух факторов: наличия движения материи в области формирования вихревой структуры и поступления межзвездного вещества как топлива на поверхность звезды. Основные положения предложенной модели можно взять за основу описания формирования звездных систем, движение которых зависит от совместного влияния отдельных вихревых структур, формирующих Галактику.
Из проведенного анализа можно сделать следующие выводы. Существующий математический аппарат недостаточен для детального изучения циркуляционных процессов, так как исходные уравнения движения материи в трехмерном пространстве не поддаются аналитическому решению, а численные методы не могут дать детальную информацию для анализа. Вместе с тем, сочетание простейших математических выкладок с существующими экспериментальными исследованиями могут послужить основой для формирования корректных гипотез, прокладывающих путь к познанию естественных законов.
ЛИТЕРАТУРА
1. Шило Н.А., Латкин А.С. Интерпретация движения планетных систем на основе модели квазипотенциального вращения // Колымские вести. № 5. 1999. С.10-12.
2. Латкин А.С. Научные и технологические основы повышения эффективности переработки тонкодисперсного сырья на базе вихревых устройств. Диссертация доктора наук. Хабаровск. 1993. 387 с.
3. Кутепов А.М., Латкин А.С., Потапов В.В. Движение и массообмен капли жидкости в закрученном потоке геотермальной среды // Теоретические основы химической технологии. М.: 2000. Т. 34. № 2. С.6-14.