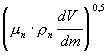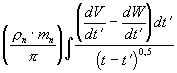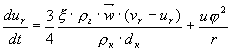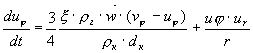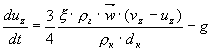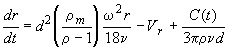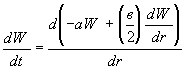В
настоящей работе на основании собранного
авторами материала и сопоставления его с
результатами предыдущих исследований
предлагается возможное объяснение
механизма и некоторых особенностей
динамики извержения и, в частности,
баллистики разлета обломков.
Общие
представления и сводные данные о таких
извержениях, а также оценки ряда главных
параметров, в частности, соотношения
контактирующих воды и магмы и диапазон
начальных скоростей пирокластических
фрагментов приведены в работах [11,13].
Сопоставляя результаты
работ предыдущих исследователей и
собственные данные, мы представляем
последовательность извержения и некоторые
его особенности следующим образом.
В
результате сейсмической активизации
возникли трещины, по которым вода проникла
в область периферическго магматического
очага. Затем
последовал фазовый переход - испарение
какого-то объема воды, декомпрессия
магматического очага и извержение - несколько десятков следовавших
один за другим выбросов сначала
резургентного материала, состоящего из
вулканогенно-осадочного чехла над очагом, а
затем и собственно материала
магматического очага в виде пепла, шлака и
бомб базальтового состава. Ксенолиты,
преимущественно кислого состава,
представленные гранитами, гранодиоритами,
обсидианами, пемзами и туфами, составляли
порядка 3 % изверженного материала и были
вынесены на земную поверхность
в твердом, реже пластическом состоянии.
Сравнительно редко встречались пемзовые
вулканически бомбы размером до 2-х метров, в
которых наблюдались включения базальтов в
виде неровных изогнутых прослоев и
приваренных корок.
Транспортером-носителем
твердого (и пластичного) силикатного
материала была пульсирующая парогазовая
струя. Направление струи было
субвертикальным.
Возникает
вопрос, каким образом некоторые крупные
фрагменты размером до 4 метров улетели от
центра извержения почти на 1,5 км, а
бомбы среднего размера, порядка 0,2 м,
были обнаружены в 2,5 км и даже дальше от
центра извержения, если
они выбрасывались вертикально вверх на
высоту в первые километры? Каков был
механизм образования мощной парогазовой
струи и разлета изверженного материала?
На
первый взгляд, механизм выброса
эксплозивного материала парогазовой
струей достаточно прост и описан многими
исследователями. Подобные явления были во
время извержения вулкана Пематанг-Бата на
Суматре в 1933 г. [11] и других извержений такого типа [13].
Истекающая
с большой скоростью (эта скорость может
быть и сверхзвуковой, в несколько сотен м/сек)
парогазовая струя захватывает твердые
фрагменты, разгоняет их во время движения в
жерле и выносит на земную поверхность. В
отличие от снаряда в орудийном стволе, в
процессе любого, в частности,
фреатомагматического извержения твердые
фрагменты не занимают все сечение жерла, и
между ними и газовой струей существует
градиент скоростей тем больший, чем больше
размер фрагментов и, соответственно, меньше
их удельная поверхность (вообще, очевидно,
существует некоторое оптимальное
соотношение размера вулканических “снарядов”
и дальности их разлета, не считая мелких и
легких фракций пеплов, способных двигаться
с воздушными потоками на расстояние в сотни
км, подобно кристалликам льда в облаке). По
расчетам С.А.Федотова, максимальная
начальная скорость вулканических бомб при
извержении в кальдере Академии Наук могла
достигать 120 м/с.
Обратим
внимание на одну из главных особенностей
извержения. Это мощные вихревые потоки,
сопровождающие, очевидно, любое
вулканическое извержение и особенно хорошо
проявляющиеся при фреатомагматическом
извержении, с участием больших масс воды,
парогазовой смеси в условиях резких
перепадов (градиентов) температуры,
давления и скорости вовлеченного в процесс
извержения материала.
Физико-механические
свойства изверженного 02.01.96 г. из кальдеры
Академии Наук материала весьма
примечательны. Бомбы базальтового состава
были обычно весьма пористы, их объемный
вес, по нашим определениям, ~ 1,2 г/см3,
при удельном весе порядка 2,8 г/см3,
свойственном базальтам. В этой связи можно
сопоставить визуально и петрохимически
близкие к исследуемым фрагменты
изверженных пород из маара озера Дальнее (Узон),
которые также имеют очень малый обьемный
вес (~1 г/см3) и плавают некоторое время
в воде. Очевидно, подобные
физико–механические свойства изверженных
пород в зачительной мере были обусловлены
субаквальным (суртсейским) типом
извержения.
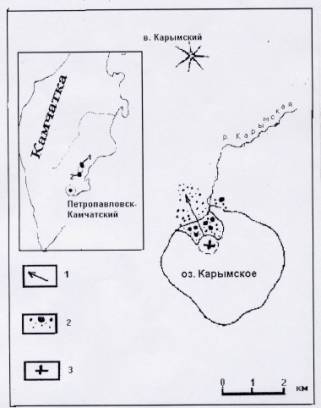
По
нашим наблюдениям, распределение
изверженного материала было неравномерным.
К западу, северо-западу от центра
извержения в кальдере Академии Наук этого
материала было немного меньше, чем к северу,
северо-востоку. Особенности
распространения эксплозивного материала
на земной поверхности (Рис.1, табл.1) дают
возможность усомниться в чисто струйном
механизме выброса пирокластики. Возможно, в
какой-то мере на формирование
эксплозивного потока оказывала влияние
водная среда, через которую проходил
вулканогенный материал. Рассмотрим
подробнее этот аспект.
Дело в
том, что прохождение высокотемпературных
масс через водную поверхность связано с
резким увеличением доли водяных паров в
продуктах выброса, что приводит, по всей
видимости, к явлению, аналогичному
формированию циклонов. Однако, учитывая
значительно более высокие градиенты
температур и локализованные
зоны формирования потока при субаквальном
извержении, удельная энергия явления (отношение
общей энергии явления к площади его
формирования) на 2-3 порядка выше, чем при
циклонической деятельности.
Таблица. Распределение
пирокластического материала вокруг центра
извержения, произошедшего 02.01.96 в кальдере
Академии Наук
Примечание. Данные, приведенные в
таблице, осреднены. В первой строке в
интервал 0-500 м. входит конус, большая часть
которого находится под водой. Мощность
пирокластики на конусе достигает 50 м [12]. Во
второй строке в 500 - 1000 м мощность определена
по обрывам реки Карымской, промывшей
возникшую при извержении.плотину из
пирокластики. (рис 2). В третьей строке в
1000-1500 м учтен самый
крупный из обнаруженных обломков размером
в 4 м на расстоянии 1,4 км от кратера Токарева.
Возможно, самый большой на таком расстоянии
от центра извержения. В
четвертой строке средняя мощность
определена по отдельным бомбам извержения
кратера Токарева, встречавшимся не более 1
бомбы на 100 м2.
Механизм
формирования "вулканогенного циклона"
следующий: парогазовый поток устремляется
вверх под действием градиента давления и
разности плотностей парогазового потока.
Создается парогазовый столб высотой в
несколько километров, по мере движения
потока в нижней его части происходит
сепарация дисперсной фазы. По периферии
потока по всей его высоте происходит
конденсация паров из-за охлаждения от
взаимодействия с окружающим воздухом. В
результате этого, парогазовый столб
окружен клубами конденсирующегося пара,
температура которого ниже температуры в
центре движущегося потока. В результате
возникшей разности плотностей между
центральной и периферийной частями потока
и формируется цилиндрическая
клубообразная структура, которая очень
хорошо просматривается на фотографиях [13].
Вместе с тем, вертикальный подъем
значительных масс парогазового потока
создает условия движения окружающих масс
воздуха по направлению к самому
парогазовому столбу из-за градиента
давления, в результате чего формируется
закрученный поток воздуха, который
вовлекает во вращение исходный поток.
Следует
отметить, что вихревая структура
сохраняется и при отсутствии взрывов, для
этого достаточно иметь участок нагретой
воды, обеспечивающей необходимый градиент
температур. В этом случае модуль вектора
пространственного вихря будет иметь
меньшие значения. Формирование вихревого
процесса происходит за счет энергии
фазового перехода, происходящего
при конденсации водяных паров. В результате
конденсации происходит резкое уменьшение
удельных объемов в области потока, а
следовательно рост градиента давления в
зоне формирования вихревой структуры.
Наличие тангенциальной составляющей
вектора скорости вихревого потока
обуславливает поле центробежных сил,
которые, суммируясь с составляющей
струйного движения при эксплозивном
выбросе, увеличивают
радиальный перенос дисперсного материала
на значительные расстояния и оказывают
сепарационное действие на
фракционирование пирокластического
материала.
Попробуем
доказать данную гипотезу. Для этого
проанализируем силы, действующие на
эксплозивный материал, построим простейшую
математическую модель и сравним результаты
расчетов с полевыми наблюдениями.
При
движении изверженного материала в паро-газовом
потоке на каждый кусок эксплозивного
материала действует сумма сил [3]:
Fк=F1+F2+F3+F4+F5+F6+F7+
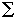 Fi .
(1)
Fi .
(1)
Рассмотрим
наиболее значимые из них:
F1 -
сила тяжести фрагмента пирокластики
F1 = vч ( rк
- rn)g,
(2)
где vч-объем
фрагмента; rк,
rn-
плотность фрагмента и потока; g -
ускорение свободного падения;



F2 -
сила, обусловленная градиентом давления в
потоке:
F2
=rч
W
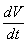 (3)
(3)
где V,W -
скорости потока и отдельного фрагмента;
t -
время;
F3 -
сила, обусловленная вращением фрагмента из-за
градиента скорости обтекающего потока и
направленная в сторону повышения скорости (сила
Магнуса),
F3 =
1,62 |V-W|dч2
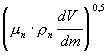 (4)
(4)
где mг
-
динамическая вязкость; m - координата
максимального температурного градиента по
отношению к фрагменту изверженного
материала; V,W - значения векторов скоростей
потока и фрагментов материала.
F4 -
сила гидродинамического сопротивления
фрагмента материала:
F4 = 0.5
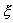 Sмrn
(V - W)|V-W|,
(5)
Sмrn
(V - W)|V-W|,
(5)
где
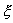 -коэффициент
гидродинамического сопротивления; Sм -
миделево сечение фрагмента;
-коэффициент
гидродинамического сопротивления; Sм -
миделево сечение фрагмента;
F5 -
сила, отражающая ускорение слоев потока,
прилегающих к поверхности фрагмента:
F5 = 0.5vк×rп 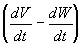 .
(6)
.
(6)
F6 -
сила, обусловленная нестационарностью
процесса и зависящая от характера движения
фрагмента за предшествующий отрезок
времени t (сила Бассе):
F6 =6Sм
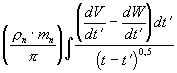 (7)
(7)
F7
-
сила, обусловленная инерцией вытесненного
фрагментом объема потока:
F7 =0,5rк
vк

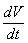 .
(8)
.
(8)
Кроме
перечисленных, на движение фрагмента
должны оказывать влияние силы,
обусловленные пульсациями газового потока,
диффузией компонентов в потоке,
электростатические силы и т.д.
Ориентировочные
расчеты показывают, что из всех сил,
оказывающих влияние на движение фрагмента
эксплозивного материала, с учетом
физических характеристик эксплозивного
потока, наиболее значимы
силы газодинамического сопротивления и
силы тяжести.
Учитывая
этот факт, движение отдельного фрагмента
эксплозивного материала в пространстве со
временем можно представить в форме
обыкновенного дифференциального уравнения
в виде:
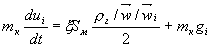 ,
(9)
,
(9)
где ui
- компоненты скорости фрагмента в
декартовой системе координат,
t
- временная переменная, mк
- масса фрагмента, mк
= rк
. pd
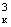 /6, rк
- плотность вещества фрагмента, dк
- эффективный диаметр фрагмента, wi -
компоненты относительной скорости
фрагмента,
/6, rк
- плотность вещества фрагмента, dк
- эффективный диаметр фрагмента, wi -
компоненты относительной скорости
фрагмента, 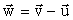 ,
, 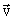 - вектор скорости газового потока, rг
- плотность пара, Sм
- площадь миделева сечения сферического
фрагмента, Sм
= pd
- вектор скорости газового потока, rг
- плотность пара, Sм
- площадь миделева сечения сферического
фрагмента, Sм
= pd
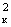 /4, x(Re)
- коэффициент сопротивления фрагмента, Re - число Рейнольдса относительного
движения, Re =
rгwdк/mг,
mг
– динамическая вязкость газа,
gi -
компоненты вектора ускорения свободного
падения.
/4, x(Re)
- коэффициент сопротивления фрагмента, Re - число Рейнольдса относительного
движения, Re =
rгwdк/mг,
mг
– динамическая вязкость газа,
gi -
компоненты вектора ускорения свободного
падения.
Анализ
наглядного материала формы взрыва,
представленный на ряде фотографий [13],
говорит о целесообразности преобразования
уравнения (4) в цилиндрическую систему
координат, что дает преимущество при
получении методами Рунге-Кутта интегралов
по времени. Разделив
обе части уравнения (9) на
mк,
получаем следующую систему уравнений:
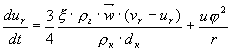 ,
(10)
,
(10)
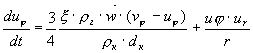 ,
(11)
,
(11)
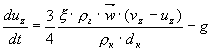 ,
(12)
,
(12)
где ur,
uj,
uz, vr,
vj,
vz,`w
- соответственно радиальная,
тангенциальная и аксиальная компонента
скорости фрагмента пирокластики,
парогазового потока и вектор относительной
скорости.
В
качестве модельного распределения вектора
скорости газа в вихревом потоке
использовали распределение, предложенное в
работе [4]:
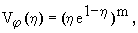 (13)
(13)
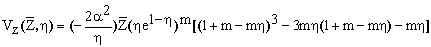 (14)
(14)
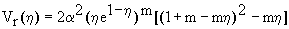 .
(15)
.
(15)
где Vj,
Vz, Vr
- безразмерные значения
составляющих вектора скорости (Vi=vi/Vjmax),
h
- значения безразмерного текущего радиуса, a2
- параметр характеризующий турбулентную
структуру потока, определяли согласно
существующей методике [5], m
- степенной коэффициент, учитывающий
структуру потока, в моделировании
материалов данных исследований m
= 1.
Для
определения значений коэффициента
сопротивления движению капли в потоке
применялось уравнение Тодеса справедливое
в диапазоне всех режимов обтекания [3]:
x
=
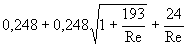 .
(16)
.
(16)
Наличие
дисперсной эксплозивной среды в потоке
оказывает влияние на изменение вязкости
потока, которое можно рассчитать по
уравнению (6):

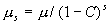 ,
(17)
,
(17)
где С -
объемная концентрация (отношение объема
эксплозивного материала к полному объему
суспензии); s-константа, равная 2,5 для
сферических бомб.
Представив
закон движения двухфазной среды в
цилиндрических координатах численным
методом, можно рассчитать траектории
движения дисперсной среды в окружающем
пространстве и, в конечном счете,
рассчитать зоны осаждения обломков на
земную поверхность.
Имеет
смысл учитывать случайное воздействие на
траектории движения отдельных фрагментов
эксплозивного материала в результате их
столкновения [4]. В этом случае
установившееся радиальное движение
летящих вулканических бомб может быть
представлено уравнением:
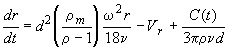 ,
(22)
,
(22)
где
w
-
угловая скорость;
V -
радиальная скорость;
r -
радиус вращения;
C(t) - коэффициент
случайного воздействия.
Составление
уравнения основано
на следующих допущениях: не учитываются
относительное движение бомб в окружном
направлении, кориолисова и относительная
силы инерции, а также составляющая
сопротивления от нестационарности
движения частицы. Согласно данным работы [5]
случайное воздействие является
дельтакоррелированной функцией времени с
нулевым средним значением, а поэтому
случайное движение частицы может быть
охарактеризовано одномерной плотностью
вероятности W (t, r).
Плотность
вероятности W
определяет концентрацию частиц в сечении r
в момент времени t,
которая находится из решения уравнения
Колмогорова-Фоккера-Планка:
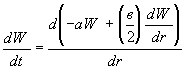 ,
(23)
,
(23)
где а=d2(
rт/r-1)
w2r/18n
-
коэффициент, характеризующий
интенсивность осаждения бомб в
центробежном поле; в=в0/(9p2r2n2d2)
-
коэффициент определяющий меру
неупорядоченности движения бомб в
результате случайных воздействий; в0
-
коэффициент интенсивности случайных
воздействий.
Предложенная
гипотеза подтверждается качественным
согласованием, результатом просчета
предложенной модели и реальным
распределением пирокластического
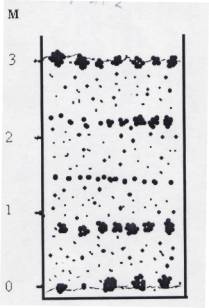
материала вокруг центра извержения (рис.5).
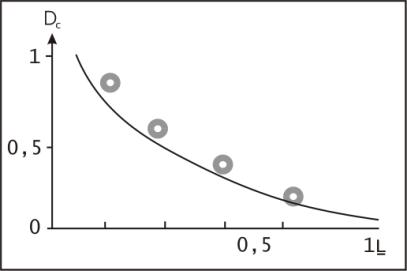
Рис.5. Сопоставление результатов
расчета с распределением
пирокластического материала, где Dc
- средний безразмерный диаметр фрагмента, L
– безразмерное расстояние.
 - результаты расчета математической
модели;
- результаты расчета математической
модели;
 - реальное
распределение пирокластического материала.
- реальное
распределение пирокластического материала.
Учет в
модели сил, связанных с наличием градиента
температур и увеличения объема из-за
фазового перехода объемов воды в
эксплозивном потоке, позволил бы
усовершенствовать предлагаемую модель и
получить более точные расчеты траекторий
обломков. К сожалению, отсутствует
возможность получения подобных данных,
основанных на прямых измерениях этих
параметров. Введение же этих параметров на
основании общих рассуждений или анализа
расчетов моделей вряд ли улучшит качество
модели. На расчеты качества
перераспределения материала эти параметры,
по нашему мнению, оказывают незначительное
воздействие и лежат в пределах случайных
явлений процесса.
Вместе
с тем отсутствие измерений скорости
движения обломков пирокластического
материала совершенно не позволяет провести
точный количественный расчет. Конечно,
можно какими-то аналитическими методами
рассчитать составляющие вектора скорости
потока, а затем ввести в модель, но учитывая,
что используемые модели аналогичны
предлагаемым, это будет очень грубый,
некорректный подход, в результате которого
получится неопределенное решение. Поэтому
на основании имеющихся данных можно
рассчитать только качественную картину
перераспределения пирокластического
материала, представив расчеты в
безразмерном виде. Для сопоставления
результатов необходимо свести к
безразмерному виду
и результаты наблюдений: 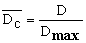 - средняя величина
безразмерного диаметра обломка;
- средняя величина
безразмерного диаметра обломка;
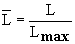 - величина
безразмерного расстояния от центра
извержения.
- величина
безразмерного расстояния от центра
извержения.
Отклонение
расчетных данных от наблюдаемых (рис.5)
объясняется, в первую очередь,
неправильностью геометрических форм
обломков, в то время как в математической
модели заложена сферическая форма частиц
дисперсного материала. Вместе с тем
качественная сходимость результатов
наблюдений и расчетов дают основание для
учета центробежных сил в аналогичных
природных явлениях.
ЛИТЕРАТУРА
1.
Большая
советская энциклопедия. 1957. № 46. С.609-612.
2.
Байков А.И.
Развитие представлений о рудоносности
структур (В печати).
3.
Кутепов А.М.,
Латкин А.С., Потапов В.В. Движение и
массообмен капли жидкости в закрученном
потоке геотермальной среды // Теоретические
основы химической технологии. М.: 2000. Т. 34. №
2. С.1-8.
4.
Кутепов А.М.,
Латкин А.С. Вихревые процессы для
модификации дисперсных систем. М.: Наука, 1999.
270 с.
5.
Латкин А.С.
Вихревые процессы для модификации
дисперсных сред. Владивосток. Изд-во ДВО РАН.
1998. 190 с.
6.
Леонов В.Л.
Поверхностные разрывы, связанные с
землетрясением и извержениями,
произошедшими в Карымском вулканическом
центре 1 -2 января 1996 г. // Вулканология и
сейсмология. 1997. № 5. С.113–130.
7.
Ли Сы Гуан.
Вихревые структуры Северо–Западного Китая.
М., 1958.
8.
Магуськин М.А.,
Федотов С.А., Левин В.Е., Бахтиаров Б.Ф.
Деформации земной поверхности в связи с
сейсмической и вулканической активностью в
Карымском вулканическом центре в январе 1996
г. // Вулканология и сейсмология.1997. № 5. С.97-113.
9.
Мелекесцев И.В.
Вулканизм и рельефообразование. М.: Наука,
1980. 210 с.
10.
Муравьев Я.Д.,
Федотов С.А.,Будников В.А., Озеров А.Ю.,
Магуськин М.А., Двигало В.Н., Андреев В.И.,Иванов
В.В., Карташова Л.А., Марков И.А. Вулканическая
деятельность в Карымском центре в 1996 г.:
верншинное извержение Карымского вулкана и
фреатомагматическое извержениев кальдере
Академии Наук // Вулканология и сейсмология.
1997. № 5. С 38-71.
11.
Ритман А.
Вулканы и их деятельность. М.: Мир, 1964. 437 с.
12.
Ушаков С.В.,
Фазлуллин С.М. Морфометрические
характеристики Карымского озера в связи с
подводным извержением // Вулканология и
сейсмология. 1997. № 5. С.130-138.
13.
Федотов С.А. Об
извержениях в кальдере Академии Наук и
Карымского вулкана на Камчатке в 1996 г., их
изучении и механизме // Вулканология и
сейсмология. 1997. № 5. С.3-38.