Рассмотрим цепочку по-прежнему одинаковых по размерам шаровых блоков, R0 = 105м, которые вращаются неоднородно. Формально такое движение блока можно смоделировать путем добавления в уравнение (2.4.28) члена d(x)msinq, который, по сути, является вынуждающей силой. Сила трения при относительном смещении блоков, как принято в задачах механики, примем пропорциональной скорости ¶q/¶h. Тогда в рамках модели неравномерного поворота с трением уравнение движения блока запишется в виде:
![]() (3.1.1)
(3.1.1)
где a - коэффициент трения, m - параметр, характеризующий вынуждающую силу, вызывающую неоднородное вращение блока, d(x) - дельта функция. Уравнение (3.1.1) получило название возмущенного уравнения СГ. Многочисленные примеры использования возмущенного уравнения СГ, как модельного уравнения движения в сейсмо-тектонических задачах, приведены в обзоре работы (Быков, 2000 а).
В отличие от невозмущенного уравнения (2.4.28) уравнение (3.1.1) не имеет аналитического решения. Численное решение возмущенного уравнения СГ (3.1.1) основано на использовании метода Маклафлина-Скотта и Рунге-Кутта (Salterno et. ol, 1983), суть которого заключается в том, что при использовании функции Грина решение возмущенного уравнения СГ структурно совпадает с (2.4.31), но координата Х и скорость u зависят от времени и связаны соотношением:
![]()
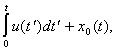
![]()
Подстановка этого соотношения и (2.4.31) в (3.1) дает систему уравнений:
![]()
![]()
Безразмерные координаты Х и скорости u рассчитывались с помощью последних соотношений методом Рунге-Кутта, а затем подставлялись в (2.4.31).
Начальные условия х0 = 0, t0 = 0,
u0 = 10-10 (u = V/c0 - безразмерная
скорость) выбирались
таким образом, чтобы скорость
деформирования не превышала значения ![]() 0 £ 10-13 с-1, что близко
средней скорости деформации в
сейсмоактивных (Родионов, Сизов, Цветков,
1986) и вулканических (Мелекесцев, 1979)
областях и заметно отличается от
глобальной средней скорости деформации (вращения
отдельных блоков) в различных регионах
Земли, оцениваемой величиной 5,5×10-16
с-1 » 1-2 град/млн. лет (England, Molnar, 1997). Следует
отметить, что значение скорости 10-13 с-1
по порядку величины близко
теоретической модельное оценке величины
угла b0 » 10-2 град. (2.4.18), на который
в рамках ротационной модели поворачивается
«элементарный» сейсмофокальный блок между
двумя последовательными во времени
сильнейшими землетрясениями с очагами в
его пределах.
0 £ 10-13 с-1, что близко
средней скорости деформации в
сейсмоактивных (Родионов, Сизов, Цветков,
1986) и вулканических (Мелекесцев, 1979)
областях и заметно отличается от
глобальной средней скорости деформации (вращения
отдельных блоков) в различных регионах
Земли, оцениваемой величиной 5,5×10-16
с-1 » 1-2 град/млн. лет (England, Molnar, 1997). Следует
отметить, что значение скорости 10-13 с-1
по порядку величины близко
теоретической модельное оценке величины
угла b0 » 10-2 град. (2.4.18), на который
в рамках ротационной модели поворачивается
«элементарный» сейсмофокальный блок между
двумя последовательными во времени
сильнейшими землетрясениями с очагами в
его пределах.
При этом скорость распространения локализованной волны уже не является величиной постоянной и кроме угловой скорости вращения тела W зависит также и от параметров a и m.
Решения
для расстояния Х, пройденного волной,
величины ее скорости V = dX/dt и величины
угловой скорости поворота блока (скорости
деформации)![]() = dq/dt при значениях параметров a » 0,1 - 1 и m
» 10-4 - 10-2, близкими
для реальных разломов (Кулагин, Маламуд,
Старков, Кулагина, 1980), как функции времени
приведены на рис.3.1.1. Из данных, приведенных
на этом рисунке, видно следующее.
Зависимости X(t) представляют собою
монотонные функции, имеющие «излом» в
точках tх и затем плавно выходящие на
асимптотику (а) Ха. Зависимости V(t)
имеют точки tVmax, в которых скорость
волны достигает своего максимального
значения Vmax, после чего плавно
выходит на асимптотику Vа.
Зависимости
= dq/dt при значениях параметров a » 0,1 - 1 и m
» 10-4 - 10-2, близкими
для реальных разломов (Кулагин, Маламуд,
Старков, Кулагина, 1980), как функции времени
приведены на рис.3.1.1. Из данных, приведенных
на этом рисунке, видно следующее.
Зависимости X(t) представляют собою
монотонные функции, имеющие «излом» в
точках tх и затем плавно выходящие на
асимптотику (а) Ха. Зависимости V(t)
имеют точки tVmax, в которых скорость
волны достигает своего максимального
значения Vmax, после чего плавно
выходит на асимптотику Vа.
Зависимости ![]() (t) имеют два четко выраженных максимума
(t) имеют два четко выраженных максимума![]() max1(tqmax1)
<
max1(tqmax1)
< ![]() max2(tqmax2),
которые разделены минимумом
max2(tqmax2),
которые разделены минимумом ![]() min(tqmin) <<
min(tqmin) <<![]() max1, tqmax1
< tqmin < tqmax2;
затем зависимость
max1, tqmax1
< tqmin < tqmax2;
затем зависимость
![]() (t) плавно выходит на асимптотику
(t) плавно выходит на асимптотику
![]() а,
а, ![]() min <
min <
![]() a <
a <
![]() max1.
max1.
Анализ
численных решений уравнения (3.1.1)
показывает следующее (Викулин, Быков,
Лунева, 2000). Во-первых, скорости Va ¸
Vmax = (10-4 ¸
4×10-2) м/с
» 1 ¸ 103 км/год
изменяются в значительных пределах и
включают весь диапазон изменения значений
скоростей уединенных волн миграции и
деформации (табл. П.2.1, П.2.3). Во-вторых,
значения максимумов скоростей деформации
составляют (0,02-3,1)×10-5 с-1 и согласуются
с наблюдениями в очагах сильных
землетрясений (Кулагин, Маламуд, Старков,
Кулагина, 1980). При
этом минимальные
значения ![]() min фиксируются
на уровне 10-9 - 10-7с-1, на ко-
min фиксируются
на уровне 10-9 - 10-7с-1, на ко-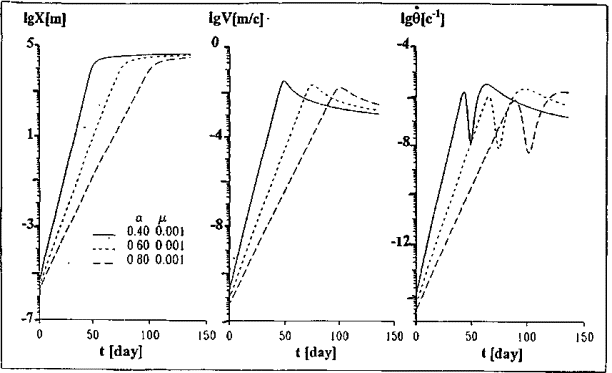
Рис.
3.1.1. Решения уравнения (3.1.1) для расстояния Х,
пройденного волной, величины ее скорости V=dX/dt и
величины угловой скорости поворота блока (скорости
деформации) ![]() =dq/dt при
значениях параметров a » 0,1 - 1,0
и m
» 10-4
- 10-2.
=dq/dt при
значениях параметров a » 0,1 - 1,0
и m
» 10-4
- 10-2.
тором изменение скорости деформирования практически не влияет на прочность горных пород.
Как видим, модельные решения не противоречат физическим условиям, определяющим течение сейсмического процесса. Следует отметить, что значения Vmax не зависят от величины начальной скорости u0 и с увеличением последней достигаются при меньших временах tVmax.
Примеры других численных решений уравнения (3.1.1) приведены в Приложении 3.
Из
данных, представленных на рис. 3.1.1, также
видим, что в отличие от равномерного
движения блоков, описываемого уравнением
СГ (2.4.28), для которого скорости V и ![]() являются
постоянными, решения уравнения (3.1.1)
являются функциями времени. Более того, все
три решения X(t), V(t) и
являются
постоянными, решения уравнения (3.1.1)
являются функциями времени. Более того, все
три решения X(t), V(t) и ![]() (t) обнаруживают такие свойства, которые
позволяют установить физически прозрачные
взаимосвязи между движениями
сейсмофокальных блоков и распространением
тектонических волн.
(t) обнаруживают такие свойства, которые
позволяют установить физически прозрачные
взаимосвязи между движениями
сейсмофокальных блоков и распространением
тектонических волн.
Во-первых, все три зависимости при малых временах изменяются по одному экспоненциальному закону
X »
X0eat, V = V0eat »
aX0eat, ![]() =
=![]() eat (3.1.2)
eat (3.1.2)
и при больших - выходят на
асимптотику. Причем выход кривых V(t) и ![]() (t) на асимптотику происходит также примерно
по одному и тому же закону. Эти данные
указывают на то, что распространение
тектонической волны, описываемое
зависимостями X(t) и V(t), и движение
сейсмофокального блока, характеризуемое
зависимостью
(t) на асимптотику происходит также примерно
по одному и тому же закону. Эти данные
указывают на то, что распространение
тектонической волны, описываемое
зависимостями X(t) и V(t), и движение
сейсмофокального блока, характеризуемое
зависимостью ![]() (t), по сути, представляют одно явление -
процесс их взаимодействия. При этом,
значение Ха оказывается близким
размеру модельного блока R0:
(t), по сути, представляют одно явление -
процесс их взаимодействия. При этом,
значение Ха оказывается близким
размеру модельного блока R0:
Xa » 105 м = R0 (3.1.3)
что позволяет конкретизировать взаимодействие и интерпретировать его как результат «захвата» тектонической волны сейсмофокальным блоком (Викулин, 1999).
Во-вторых, особые, минимаксные моменты времени для всех трех решений, т.е. моменты, характеризующие как движение блока, так и распространение волны, оказываются близкими друг другу:
tX » tVmax » tqmin = t0 (3.1.4)
и при постоянных r, G, R0 и W для всех блоков цепочки) полностью определяются значениями параметров a и m:
t0 = t0(a, m) (3.1.5)
Эти данные позволяют предположить, что взаимодействие тектонической волны с сейсмофокальным блоком в окрестности точки t0 имеет такую особенность, которую аналитически можно описать с помощью параметров a и m.
В-третьих,
отношение продолжительностей максимумов Dtqmax1,2
и их амплитуд ![]() max1,2 во всем исследуемом диапазоне
параметров a и m не зависят от их значений, т.е.
являются постоянными величинами:
max1,2 во всем исследуемом диапазоне
параметров a и m не зависят от их значений, т.е.
являются постоянными величинами:
Dtqmax2/Dtqmax1 = 6 ± 2 (3.1.6)
![]() max2/
max2/![]() max1
= 2 - 2,5
(3.1.7)
max1
= 2 - 2,5
(3.1.7)
Эти данные позволяют
предположить, что первый (t < t0) и
второй (t > t0)
максимумы функции ![]() (t) соответствуют разным стадиям
взаимодействия. Назовем их соответственно
первой и второй стадиями взаимодействия.
(t) соответствуют разным стадиям
взаимодействия. Назовем их соответственно
первой и второй стадиями взаимодействия.
Из опытов по деформированию горных пород (Соболев, 1993) следует, что «пикообразные выбросы скорости деформаций соответствуют ускорению деформации» и сбросу нагрузки. Таким образом, полученные выше результаты оказывается возможным проинтерпретировать следующим образом: особенностью взаимодействия, по сути, является высвобождение накопленных напряжений или землетрясение, которое происходит в результате локализации неустойчивой деформации в момент времени t0. Следовательно, первой и второй стадией взаимодействия тектонической волны с сейсмофокальным блоком, по сути, должны являться форшоковая и афтершоковая стадии сейсмического цикла. Покажем это.
Особенности
распределения форшоков и афтершоков в
очагах сильнейших курило-камчатских и
японских землетрясений исследовались в
работе (Викулин, Викулина, Митякин, 1991) и
приведены в Приложении 1. Данные о
магнитудах и временах наиболее сильных из
них суммированы в таблице 3.1.1. Видно, что
интервалы времени, в течение которых
форшоки и афтершоки происходят
относительно сильнейших толчков,
соотносятся в пропорции Dta/Dtф
= 69/11 = 6,3, близкой отношению
продолжительностей максимумов скорости
деформации ![]() (3.1.6). В то же время,
при близости значений магнитуд наиболее
сильных форшоков и афтершоков: Мф » Ма, их числа Na и Nф, а,
следовательно, и суммарные сейсмические
энергии Еа и Еф, выделяемые в
течение форшоковой и афтершоковой стадий,
соотносятся между собою в пропорции Na/Nф
= Еа/Еф = 2,3, близкой отношению
величин максимумов скоростей деформации
(3.1.6). В то же время,
при близости значений магнитуд наиболее
сильных форшоков и афтершоков: Мф » Ма, их числа Na и Nф, а,
следовательно, и суммарные сейсмические
энергии Еа и Еф, выделяемые в
течение форшоковой и афтершоковой стадий,
соотносятся между собою в пропорции Na/Nф
= Еа/Еф = 2,3, близкой отношению
величин максимумов скоростей деформации![]() (3.1.7). На наш взгляд,
приведенные данные о форшоках и афтершоках
в очагах сильнейших землетрясений и
результаты проведенного сравнительного
анализа, являются сильным аргументом в
пользу сформулированного выше
предположения о том, что первый и второй
максимумы на кривой
(3.1.7). На наш взгляд,
приведенные данные о форшоках и афтершоках
в очагах сильнейших землетрясений и
результаты проведенного сравнительного
анализа, являются сильным аргументом в
пользу сформулированного выше
предположения о том, что первый и второй
максимумы на кривой ![]() (t), по сути, соответствуют форшоковой и
афтершоковой стадиям сейсмического
процесса.
(t), по сути, соответствуют форшоковой и
афтершоковой стадиям сейсмического
процесса.
Таким образом, показано, что ротационная модель, в принципе, позволяет количественно описать такие важные свойства сейсмического процесса, как его форшоковую и афтершоковую стадии и заключенную между ними «особенность» - сильнейшее землетрясение.
Любое волновое взаимодействие, согласно законам механики, осуществляется в соответствии с теми или иными вариационными принципами и проявляется в виде определенных закономерностей, которые наблюдаются при изменении определяющих задачу параметров в пределах многих порядков по величине. В одномерном случае уравнение СГ, как известно (Скотт, Чжу, Маклафлин, 1973), относится к классу интегрируемых уравнений, для которых в явном виде существует и функция Лагранжа и интегралы (законы) сохранения. Физический смысл волновых решений, получаемых в рамках ротационной модели с помощью уравнения СГ, был продемонстрирован в предыдущей части на примерах, в которых дано объяснение спектра скоростей миграции сейсмичности (2.4) и природы колебаний Чандлера (2.5), и выше в этой части, на примере форшоковой и афтершоковой стадий сейсмического процесса. Таким образом, решения уравнения 3.1.1, представленные на рис. 3.1.1, должны адекватным образом описывать процесс взаимодействия тектонической волны с блоками сейсмофокальной зоны при изменении параметров модели a и m в пределах многих порядков их величины.
С целью поиска законов такого взаимодействия решения модельного уравнения (3.1.1) исследовались в широком диапазоне определяющих задачу параметров a > 0 и m > 0, значения которых изменялись в пределах восьми-девяти порядков, включая рассмотренный выше диапазон : 10-5 £ a £ 102-3, 10-5 £ m £ 102-3. Шаг изменения параметров составлял один порядок. Решения представлены на рис. 3.1.2. Видно, что решения могут рассматриваться как непрерывные функции параметров a и m в широком диапазоне.
Таблица 3.1.1.
Данные о магнитудах и временах наиболее сильных форшоков (ф) и афтершоков (а) с М³7, происшедших в очагах сильнейших северо-западно-тихоокеанских землетрясений 1900-1980 гг.
|
Сильнейшее землетрясение |
Форшок |
Афтершок |
Регион |
|
Дата М |
М lgDtф[h] |
М lgDta[h] |
|
|
25.06.1904 7,7 03.02.1923 8,5 24.02.1923 7,7 04.11.1952 8,5 04.05.1959 7,6 |
7,7 0,78 7,0 1,54 - - - |
7,3 1,43 - 7,3 3,07 7,0 3,17 7,0 3,04 |
Южная Камчатка Кроноцкий залив, Камчатка Камчатский залив, Камчатка Авачинский залив, Камчатка Кроноцкий залив, Камчатка |
04.03.1952 8,3 04.11.1952 8,5 06.11.1958 8,2 13.10.1963 8,0 11.08.1969 8,2 17.06.1973 7,9 24.03.1978 8,0 |
- - - 7,2 1,26 7,4 -2,60 - 7,8 1,61 |
7,2 2,13 7,0 3,17 7,4 2,15 7,4 2,21 7,8 -2,85 7,4 2,22 - |
о. Хоккайдо, Япония Северные Курилы о. Итуруп, Южные Курилы о. Уруп, Южные Курилы о. Шикотан, Южные Курилы Малые Курилы о.Итуруп, Южные Курилы |
|
01.09.1923 8,2 05.11.1938 7,7 07.12.1944 8,0 16.05.1968 7,9 |
- 7,1 3,60 - - |
7,3 1,38 7,5 1,08 7,1 2,94 7,5 1,00 |
Канто, Япония о. Хонсю, Япония Тонанкай, Япония о. Хонсю, Япония |
|
Число толчков Nа,ф Магнитуда
Среднее
Интервал,
D |
6 7,4±0,3 1,03±1,84
11 |
14 7,3±0,2 1,84±1,49
69 |
|
Ограничение величины параметров снизу значением 10-5 объясняется возможностями как программы расчета, так и используемого компьютера: при малых m (малой величине вынуждающей силы) процесс взаимодействия протекает очень медленно и для его расчета не хватает компьютерного времени. Поэтому при предельном преобразовании a ® 0, m ® 0, символизирующем переход описания сейсмического процесса к невозмущенному уравнению СГ (2.4.28), можно принять, что система взаимодействующих сейсмофокальных блоков переходит в режим их равномерного движения и такой переход осуществляется в течение большого (в пределе, по-видимому, бесконечного) по продолжительности интервала времени.
Ограничения сверху связаны с существованием таких (критических) значений параметров a = aкр, m = mкр, aкр = mкр = 6,34, при стремлении к которым снизу решения возмущенного уравнения СГ (3.1.1) достаточно резко (скачкообразно) переходят в решения невозмущенного уравнения СГ (рис. 3.1.3). При этом, временной интервал, в течение которого осуществляется такой переход, достаточно мал по продолжительности. Отметим, что в диапазонах изменения параметров a < aкр, 0 < m < 102-3; m < mкр, 0 < a < 102-3 решения возмущенного уравнения сохраняют свою описанную выше специфику - зависимость от времени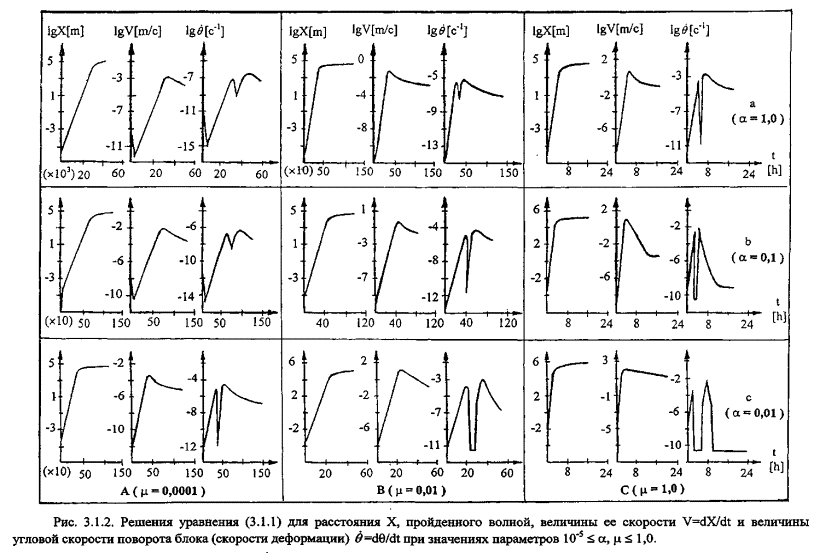
Таким образом, диапазон, в пределах которого решения возмущенного уравнения СГ (3.1.1) отличаются от решений невозмущенного уравнения СГ (2.4.28), т. е. диапазон применимости возмущенной ротационной модели, можно определить следующими пределами изменения параметров задачи:
0 < a, 0 < m < mкр; 0 < m, 0 < a < aкр (3.1.8)
В данной работе не будем останавливаться на анализе особенностей в окрестности критической точки. Отметим лишь, что объяснение особенностей сейсмического процесса в ее окрестности, скорее всего, связано со следующими примерными равенствами aкр » 2p, mкр » 2p.
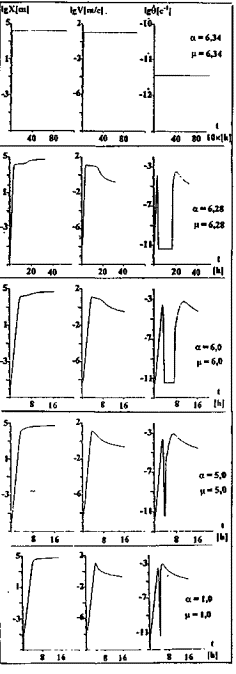
Рис.
3.1.3. Решения уравнения (3.1.1) для расстояния Х,
пройденного волной, величины ее скорости V=dX/dt и
величины угловой скорости поворота блока (скорости
деформации) ![]() =dq/dt при
значениях параметров a = m
» 1,0-6,34.
=dq/dt при
значениях параметров a = m
» 1,0-6,34.
Решения
модельного уравнения (3.1.1) - зависимости X(t) и
V(t) и ![]() (t), в диапазоне 10-5 £ a, m £ 1, представлены на рис. 3.1.2.
Решения можно рассматривать как функции
параметров a
и m. Поэтому заключенные в них
особенности можно определять через a и m. При этом, по-прежнему, при
малых (t < tVmax) временах справедливо
соотношение (3.1.2), при больших (t > tqmax2)
- имеет место выход решений на асимптотики.
Таким образом, сформулированный выше вывод
о том, что модельные решения уравнения (3.1.1)
описыват особенности взаимодействия
тектонической волны с блоками
сейсмофокальной зоны остается в силе для
всего диапазона изменения параметров (3.1.8).
(t), в диапазоне 10-5 £ a, m £ 1, представлены на рис. 3.1.2.
Решения можно рассматривать как функции
параметров a
и m. Поэтому заключенные в них
особенности можно определять через a и m. При этом, по-прежнему, при
малых (t < tVmax) временах справедливо
соотношение (3.1.2), при больших (t > tqmax2)
- имеет место выход решений на асимптотики.
Таким образом, сформулированный выше вывод
о том, что модельные решения уравнения (3.1.1)
описыват особенности взаимодействия
тектонической волны с блоками
сейсмофокальной зоны остается в силе для
всего диапазона изменения параметров (3.1.8).
Данные,
представленные на рис. 3.1.2, позволяют
высказать вполне определенные
предположения о природе особенности (неустойчивости)
сейсмического процесса, которая «заключена»
между сильными форшоками и афтершоками. А
именно, существует такая совокупность
точек (a*, m*),
связанных зависимостью a* ~ ![]() , которая «начинается»
в критической точке aкр = mкр и на
плоскости (m,a) решения модельного уравнения
(3.1.1) разделяет на два класса:
, которая «начинается»
в критической точке aкр = mкр и на
плоскости (m,a) решения модельного уравнения
(3.1.1) разделяет на два класса:
a*(m*) = ![]() »
» ![]() (3.1.9)
(3.1.9)
Отметим, что, как следует из данных, приведенных на рис. 3.1.2, в пределах узкой полосы, протягивающейся вдоль графика a*(m*), справедливо примерное равенство:
Ха » R0 ® l » l0, k » k0 (3.1.10)
символизирующее равенство протяженности сейсмофокального блока и длины взаимодействующей с ним тектонической волны.
К
первому классу относятся решения,
расположенные в левой верхней части
плоскости (a, m), особенность которых - минимум
функции ![]() (t), имеет «нулевую» по времени
продолжительность и достигает своего
максимального значения на кривой (3.1.9):
(t), имеет «нулевую» по времени
продолжительность и достигает своего
максимального значения на кривой (3.1.9):
a ³ a*, m £ m* : Dtqmin =0,![]() (3.1.11)
(3.1.11)
Ко второму - решения, расположенные в правой нижней части плоскости (m, a), особенность которых имеет не нулевую по времени продолжительность и на кривой (3.1.9) достигает своего наименьшего значения:
a < a*, m > m* : Dtqmin ¹ 0;![]() (3.1.12)
(3.1.12)
Для условий (3.1.11), как можно видеть из данных, представленных на рис.3.1.1 и 3.1.2, справедливы соотношения (3.1.3), (3.1.6) и (3.1.7).
Таким образом, можно принять, что соотношения (3.1.3), (3.1.6) и (3.1.7) описывают процессы, происходящие при взаимодействии «элементарного» сейсмофокального блока и тектонической волны. Другими словами - при землетрясении. Предельный для соотношений (3.1.11) переход: a ® a*, m ® m*, при котором неусточивость процесса максимальна, очевидно, соответствует наиболее сильному, т.е. сильнейшему землетрясению.
Как видим, совокупность точек (a*, m*), описываемая соотношением (3.1.9), по сути, является «критической», так как характеризуется максимально возможной неустойчивостью, возникающей при взаимодействии тектонической волны с сейсмофокальным блоком.
Условия (3.1.22) соответствуют случаю, при котором асимптотика функции Х(t) превышает размер «элементарного» сейсмофокального блока:
a < a*, m > m* : Xa > R0 (3.1.13)
и при значениях параметров a = 10-4-10-5, m = 0,1-1 достигают значений Ха » n×107 км, где n = 1-5. Условие (3.1.13) показывает, что в этом (3.1.12) случае решения, расположенные в правой нижней части рис. 3.1.2, в зависимости от значений Ха, описывают взаимодействие тектонической волны с несколькими блоками. При этом, как можно видеть из данных, представленных на рис. 3.1.2, имеет место зависимость:
a < a*, m > m* : Dtqmin ~ Xa. (3.1.14)
Эта зависимость указывает на то, что при взаимодействии, протекающем в пределах достаточно продолжительного отрезка времени, выделение и (или) перераспределение упругой энергии может осуществляться в виде замедленных землетрясений (Kanamori, Steward, 1979), землетрясений - дуплетов (Lay, Kanamori, 1980), крипа или волн деформации.
В верхней левой части плоскости (a, m) : a > a*, m < m*, как
можно видеть из данных, представленных на
рис. 3.1.2, справедливо соотношение Ха
< R0. При этом «амплитуда» минимума
функции
![]() (t) меньше, чем на кривой a*( m*).
(t) меньше, чем на кривой a*( m*).
Таким образом, анализ модельных решений возмущенного уравнения СГ (3.1.1) позволяют предположить следующее. Результатом взаимодействия тектонической волны с сейсмофокальными блоками могут являться: 1) сильнейшее землетрясение в случае равенства длины волны протяженности блока (3.1.10), 2) сильное землетрясение в случае меньшей длины волны и 3) медленные землетрясения или землетрясения - дуплеты в случае длины тектонической волны, большей размеров одного блока (3.1.13).
Из соотношений (3.1.2), которые, как уже отмечалось, справедливы во всем диапазоне применимости возмущенной ротационной модели, следует, что угол поворота поля упругих напряжений относительно блока пропорционален расстоянию, пройденному волной q = cX, где, c - угол кручения. Как видим, взаимодействующая с сейсмофокальным блоками тектоническая волна, по сути, является волной кручения (Викулин, Быков, Лунева, 1998, 2000).
Во всем диапазоне параметров a и m (3.1.8), как можно видеть из данных, представленных на рис. 3.1.2 и в Приложении 3 (рис. П.3.1-П.3.6), следующие величины имеют постоянные значения, т.е. являются интегралами взаимодействия (Викулин, 2000):
![]() max1×tqmax1
= const = j* = 0,73±0,06 рад = 42о±3о
(3.2.1)
max1×tqmax1
= const = j* = 0,73±0,06 рад = 42о±3о
(3.2.1)
Vmax×tVmax = const =(2,5±1,3)×105 м » 2R0 (3.2.2)
При этом, функции, описывающие моменты времени, при которых достигаются максимальные tqmax1(a,m) (рис. П.3.4), tVmax(a,m) (рис. П.3.1) и минимальное tqmin(a,m) (рис. П.3.7) значения, практически тождественны друг другу:
tqmin(a,m) » tqmax1(a,m) » tVmax(a,m) = tVq1; 10-5 £ a,m £ 1 (3.2.3)
и приближенно могут быть записаны в следующем виде:
tVq1 ¹ f(a) ; tVq1 » 3m-0,5 (3.2.4)
Тогда из соотношений (3.2.1) - (3.2.3) для угла кручения получаем величину
c = j*/R0 » 10-7 рад/см (3.2.5)
которая, очевидно, также имеет смысл постоянной взаимодействия.
Функции, описывающие параметры второго
максимума скорости деформации
![]() max2(a,m) (рис. П.3.9), tqmax2(a,m) (рис. П.3.8) и
max2(a,m) (рис. П.3.9), tqmax2(a,m) (рис. П.3.8) и ![]() max2×tqmax2(a,m) (рис. П.3.10), не соответствуют
соотношениям (3.2.1)-(3.2.4). Поэтому
установленные выше законы сохранения
выполняются только в течение первой,
форшоковой стадии взаимодействия.
max2×tqmax2(a,m) (рис. П.3.10), не соответствуют
соотношениям (3.2.1)-(3.2.4). Поэтому
установленные выше законы сохранения
выполняются только в течение первой,
форшоковой стадии взаимодействия.
Как видно из первого неравенства в соотношении (3.2.4), можно принять, что в течение первой стадии взаимодействие тектонической волны с сейсмофокальным блоком происходит без диссипации, т.е. в течение этого отрезка времени блок можно считать неподвижным. Другими словами, в течение форшоковой стадии тектоническая волна кручения взаимодействует с полем упругих напряжений, которое, в соответствии с представлениями ротационной модели, сосредоточено вокруг блока. Тогда из второго примерного равенства в (3.2.4), с очевидностью, следует увеличение интервала взаимодействия до бесконечно длинного при уменьшениим вынуждающей силы (т.е. значения m) до нуля.
Величина угла кручения, по определению (Ландау, Лифшиц, 1965), равна c = Мf/С, где Мf - момент силы, С - крутильная жесткость объема среды, в пределах которого распространяется волна. Принимая значение крутильной жесткости, равное жесткости цилиндрического слоя С = 2pGhR03 с радиусом R0 и толщиной h, для момента силы, приложенному к этому объему, получим выражение
Мf = 2pcGhR03 = 2pGhj*R02 (3.2.6)
Как видим, величина момента силы, как и c (3.2.5), j* (3.2.1) и R0 (3.2.2), также имеет смысл постоянной взаимодействия в течение первой стадии.
Значение j*, которое достигается в конце форшоковой стадии, как хорошо известно (Соболев, 1993), равно углу, под которым при сжатии образцов в лабораторных условиях проходит поверхность сдвигового разрушения. Другими словами, поворот поля упругих напряжений относительно неподвижного блока на такой угол равносилен образованию кольцевой дислокации, вектор Бюргерса которой направлен вдоль оси цепочки блоков и по величине равен D = j*R0 (Ландау, Лифшиц, 1965). Тогда выражение для момента волны (3.2.6) можно переписать в виде
Mf = GDS (3.2.7)
где S = 2pR0h - площадь сечения слоя, в пределах которого происходит взаимодействие тектонической волны кручения с полем упругих напряжений вокруг блока.
По сути, полученное в рамках ротационной модели соотношение (3.2.7) совпадает с выражением для сейсмического момента М0 (Касахара, 1985). Более того, при принятых выше значениях модельных параметров R0 и G и при h = 10-(5¸3)×R0 численное значение для момента силы волны Мf = 1028¸30 дин×см по порядку величины равно величине сейсмического момента очага для класса сильнейших тихоокеанских землетрясений (Касахара, 1985).
Таким образом, в течение первой стадии взаимодействия тектоническая волна, «закручивая» поле упругих напряжений до критического угла j*, создает условия для образования вокруг сейсмофокального блока вдоль его поверхности кольцевой дислокации. Другими словами, если края дислокации к моменту ее образования «будут готовы» сместиться друг относительно друга, то есть, если параметры, определяющие трение и вынуждающую силу, будут соответствовать зависимости (3.1.19), то в момент времени tVmax » tqmin, согласно представлениям ротационной модели, очевидно, должно произойти сильнейшее землетрясение.
Решениями линейных волновых уравнений, описывающих состояние твердого тела, являются упругие волны. В нелинейных уравнениях волновыми решениями являются другие возбуждения. В силу того, что нелинейные уравнения часто не имеют аналитического решения, описание таких возбуждений бывает затруднено. Для описания возбуждений соответствующих нелинейным уравнениям используются различные приближенные методы. Одним из таких методов является способ линеаризации уравнения.
Решения линеаризованного возмущенного уравнения СГ А.С. Давыдов (1975, 1982) назвал экситонами. Свойства экситонов, соответствующих уравнению (3.1.1), определяются дисперсионным соотношением:
![]() (3.2.8)
(3.2.8)
и групповой скоростью
U = ![]() (3.2.9)
(3.2.9)
Уравнение (3.2.8) имеет одно чисто мнимое решение:
![]() (3.2.10)
(3.2.10)
которому соответствует дисперсионное соотношение:
![]() (3.2.11)
(3.2.11)
Полученное решение соответствует экситонам с большой скоростью (энергией Е):
U ® ¥, (Eex ® ¥) (3.2.12)
и длиной волны:
l » l0, |k| » k0 (3.2.13)
Характерная скорость миграционного сейсмического процесса с0 (» 1 см/сек, см. (2.4.39)) по величине на много порядков меньше скорости упругих волн V (³ 4 км/сек). Поэтому в рамках механической здачи условие (3.2.12) всегда выполняется для экситонов со скоростями близкими скоростям упругих волн:
U ® V (3.2.14)
Другими словами, дисперсионное соотношение (3.2.11), полученное на основании анализа волновых свойств возмущенного (линеаризованного) уравнения СГ, описывает экситонные решения с длинами волн, равными размерам «элементарных» сейсмофокальных блоков, и скоростями близкими скоростям упругих волн.
Полученный результат позволяет в рамках ротационной теории связать воедино экспериментальные данные по волнам миграции афтершоков в очагах землетрясений (рис. 2.3.1) с численными решениями модельного уравнения 3.1.1, представленными на рис. 3.1.3.
Действительно, с одной стороны, стремление скорости экситонов к скорости звука, количественно описываемое соотношениями (3.2.12) и (3.2.14), равносильно предельному переходу, при котором скорость миграции афтершоков стремится к скорости распространения разрыва, т.е. излучению упругих волн при землетрясении. С другой стороны, наиболее неустойчивое состояние сейсмического процесса, которое описывается соотношениями (3.1.9) и (3.1.10) также соответствует «сбросу нагрузки» - т.е. землетрясению.
Таким образом, было показано, что
модельные «предельные» (a ® a*, m ® m*) для
первой стадии взаимодействия
тектонической волны с сейсмофокальным
блоком решения соответствуют также «предельным»
(Vex ®
V) экситонам или волнам миграции афтершоков
в очагах сильнейших землетрясений (Vex)
с максимально возможной скоростью -
скоростью распространения разрыва при
землетрясении (V). И такое решение, т.е. «предельно»
сильное или сильнейшее землетрясение в
рамках ротационной модели может произойти
только при выполнении вполне определенных
соотношений между длиной тектонической
волны l и размером сейсмофокального
блока R0: l » 2R0 = l0. Это
условие определяется соотношениями (3.1.10) и
(3.2.9), а также величинами диссипации (a) и вынуждающей силы (m):
a* » (2¸![]() )
)![]() на основании (3.1.10) и (3.2.13).
на основании (3.1.10) и (3.2.13).
Представляется, что сформулированный вывод может быть распространен на весь диапазон параметров a* £ a, m £ m*, для которого Dtqmin = 0. Действительно, для всего этого диапазона выполняются как «законы сохранения» (3.2.1) - (3.2.7), так и «необходимые» условия (3.1.9), (3.1.10) и (3.2.11), (3.2.13). При этом, сильнейшим землетрясениям соответствуют только предельные решения, на плоскости (a,m) расположенные «вдоль» зависимости a*(m*), определяемой соотношениями (3.1.9) и (3.2.11). Другим значениям параметров в этой части плоскости: a > a*, m < m*, по сути задачи должны соответствовать сильные землетрясения с размерами очага (асимптотическими значениями Ха), меньшими размера сейсмофокального блока R0: Xa < R0. Соответствующая совокупность сейсмических дыр, в таком случае, является, возможно, характеристикой структуры сейсмофокального блока, «визуализированной» в результате его взаимодействия с тектоническими волнами.
Решения, на рис. 3.1.2 соответствующие правой нижней части плоскости (a, m): a < a*, m > m*, в пределах которой тектоническая волна взаимодействует с совокупностью «элементарных» блоков (3.1.12)-(3.1.14), как представляется, реализуются на участках сейсмофокальной зоны с относительно невысоким уровнем сейсмичности. В пределах таких участков сильнейшие (М > 7,5) землетрясения, вероятно, не происходят; сброс и (или) перераспределение упругой энергии происходит в виде замедленных землетрясений (Kanamori, Steward, 1979), землетрясений-дуплетов (Lay, Kanamori, 1980), крипа или волн деформации.
В результате проведенного в настоящей работе исследования было показано следующее.
Решения модельного уравнения (3.1.1) описывают взаимодействие тектонической волны с сейсмофокальными блоками. Выявлен ряд характерных особенностей, которые позволяют установить существование двух следующих друг за другом стадий, в пределах которых взаимодействие проявляется по разному.
В течение первой, форшоковой стадии тектоническая волна является уединенным солитоном кручения, момент силы которого по порядку величины равен сейсмическому моменту очага сильнейшего землетрясения. Такая нелинейная волна (по сути «маятниковая (Курленя, Опарин, 2000)), взаимодействуя с полем упругих напряжений, «разворачивает» его относительно сейсмофокального блока, который в течение этой стадии можно считать неподвижным. Результатом «форшокового» взаимодействия является создание таких условий на поверхности блока, при которых образуется кольцевая дислокация.
В широком спектре модельных решений в течение последующей, второй, стадии показано существование волновых возмущений (по-видимому, экситонной природы) со скоростями, значения которых на много порядков превышает величину предельной тектонической скорости крипа с0. Такими (экситонными) решениями являются волны миграции афтершоков в очагах землетрясений.
Из физики твердого тела известно, что солитон при достаточно большой его энергии распадается на дислокацию и экситон (Давыдов, 1982). Другими словами, в рамках ротационной модели сильнейшее землетрясение (образование дисслокации) и афтершоковые (экситонные) движения в его очаге определяются условиями распада тектонической (уединенной) волны кручения при ее взаимодействии с соответствующим сейсмофокальным блоком.
Как видим, основная задача механики очага землетрясения в традиционной ее постановке: исследование процесса возбуждения упругих волн - является частью более общей задачи, которая может быть решена в рамках развиваемого в этой работе ротационного подхода. При этом одно их основных отличий ротационной механики очага землетрясения от общепринятой (Соболев, 1993) заключается в другой геометрии образующейся при землетрясении плоскости разрыва - дисклинация (кольцевая дислокация) вместо плоскости.
Геофизические аргументы в пользу ротационной механики, на наш взгляд, очевидны. В достаточно полном виде они представлены выше.
Достижения физики прочности, полученные в последние десятилетия, все больше склоняются к выводу о дисклинационной природе веществ, в основе которой заложены представления о существовании в деформируемом твердом теле механического самосогласованного поля, которое распространяется в виде волн смещений и поворотов (Лихачев, Панин, Засимчук, и др., 1989). При этом, наряду с обычными в теле обязательно существуют и моментные напряжения, имеющие дальнодействующий характер (Лихачев, Волков, Шудегов, 1986).
Таким образом, заложенные в основу ротационной механики сейсмотектонического процесса и очага сильнейшего землетрясения принципы представляются достаточно обоснованными и с позиции последних достижений физики твердого тела, и с точки зрения комплекса геофизических данных.
Следующие данные: 1) блоковое строение геофизической среды (Садовский, 1979; Садовский и др., 1987, 1991); 2) наличие вполне определенной физической аналогии между уединенными волнами (солитонами) и частицами (Гапонов-Грехов, Рабинович, 1979); 3) моментный характер взаимодействия тектонических волн с сейсмофокальными блоками (два предыдущих раздела настоящей главы); 4) сама возможность описания параметров сейсмичности (величины сейсмической активности, угла наклона графика повторяемости и максимальной величины энергетического класса) через квантово-механические функции Ленжевена и Планка-Эйнштейна (Левый, 2000) - позволяют предположить существование дискретной или «квантованной» составляющей у сейсмотектонического процесса. Необходимо отметить, что идея об ограниченности закона повторяемости землетрясений справа была высказана и развивалась в работах Ю.В.Ризниченко (1985).
Далее: наличие тесной взаимосвязи между сейсмическим режимом планеты и ее собственными колебаниями (Stacey,1969; Котляр, Ким, 1994; Chao, Gross, 1995; Курбасова и др., 1997); возможность описания динамики процессов, ответственных за подготовку и реализацию как отдельно взятых землетрясений, так и протекающего в пределах вращающейся неоднородной и фрактальной Земли сейсмического процесса с помощью введения гипотезы о макросейсмическом деффекте - сейсмоне (Поплавский, Соловьев, 2000) наводит на мысль о возможной ротационной природе такого рода квантовых эффектов.
Именно интуитивное ощущение обозначенных выше физически прозрачных аналогий, а не их осмысленное видение, как представляется, присутствует в ряде работ (Kanamori, 1978; Anghel, Lomnitz, 1982) и даже сборника (Quantification..., 1978) - «квантовых» по названию, и, на взгляд автора, способствовало, например, введению моментной магнитуды МW (Kanamori, 1977).
Следует отметить, что само появление гипотезы о макросейсмических деффектах, имеющих ротационную природу, в теле твердой Земли физически почти очевидно (Поплавский, Соловьев, 2000). Действительно, в масштабе геологического времени Землю, как показал О.Г.Сорохтин (1974), можно рассматривать как каплю вязкой жидкости, эллипсоидальная форма фигуры равновесия которой, согласно данным классических работ Б.Римана и П.Дирихле (Ламб, 1947; Монастырский, 1979), при определенных условиях является суперпозицией равномерного вращения и внутренних движений с равномерной завихренностью.
Фундамент под квантовую сейсмотектонику был подведен работами многих исследователей, начиная с классических работ конца 60х–начала 70х гг. прошлого века (Elsasser, 1969; Savage, 1971). В этой связи особенно следует отметить работы А.В.Николаева и В.Н.Николаевского с сотрудниками (Проблемы..., 1987; Николаевский, 1996; Хаврошкин, 1999), в которых, фактически, были заложены физические основы новых направлений: «нелинейная сейсмика» и «механика уединенных тектонических волн».
По-видимому, впервые такого рода вопросы предметно обсуждались в нескольких докладах на всероссийской конференции по проблемам сейсмичности Дальнего Востока (Петропавловск-Камчатский, 6-9 апреля 1999 г.), что позволило впоследствии, в трудах конференции, объединить их в один раздел под названием «Квантовая сейсмотектоника» (Проблемы..., 2000). Ниже будет изложена концепция автора (Викулин, 1997, 2000; Викулин, Кролевец, 2001).
Из данных, представленных на рис. 2.5.1 a, можно видеть, что траектории движения полюса планеты на плоскости XOY располагаются с разной плотностью: имеются интервалы DR, в пределах которых траектории располагаются с большей плотностью, в то время как между этими интервалами - с меньшей. Это позволяет предположить, что, возможно, существуют выделенные значения радиусов траекторий, вдоль которых полюс планеты движется более часто.
Выбор способа выявления такого рода закономерностей значительно облегчается тем обстоятельством, что экспериментальные значения каждой из координат {x, y} в отдельности, в целом, подчиняются нормальному распределению. При этом среднеквадратичные отклонения каждого из таких распределений оказались достаточно близкими: sх » sу » 0//,13 » Rср. Откуда для теоретической зависимости плотности вероятности, характеризующей распределение значений амплитуд движения полюса планеты, получаем следующее выражение: Ро(R) = (R/s2)exp(-R2/2s2), R2=x2 + y2, s = (sx + sy)/2 » sx » sy » Rср.
Свойства распределения Ро(R) хорошо известны: нулевая плотность траекторий при R = 0, затем ее монотонное увеличение до значения Rср = s, в окрестности которого плотность траекторий максимальна, после чего опять монотонное уменьшение до нуля при больших R. Как можно видеть из данных, представленных на рис. 2.5.1 а, экспериментальное распределение заметно отличается от теоретически ожидаемого.
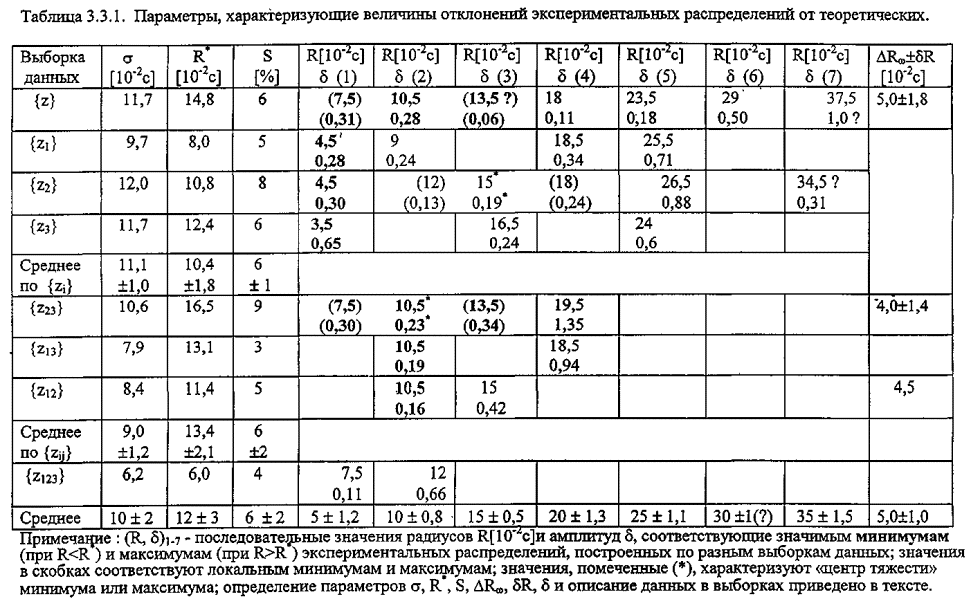
Исследовались свойства экспериментальных распределений, которые строились для разных наборов исходных данных: {z} - совокупность всех исходных данных; {zi} - с исключенной одной гармоникой, где i=(1; 2; 3) суть индексы (ch,1; ch,2; 1 - годовая гармоника) соответственно; {zij} -с двумя и {z123} - тремя исключенными гармониками. Из данных, представленных на рис. 3.3.1 и в табл. 3.3.1, видно, что для всех проанализированных совокупностей данных имеет место значимое отклонение экспериментального распределения P от теоретического P0. Это отличие проявляется в том, что существует такое значение R*, при котором Р < (£) Po при R < R* и Р > (³) Po при R > R*.
Физика выявленной закономерности, имеющей общий характер, заключается в существовании такого механизма, который перераспределяет «нутационную» энергию между колебаниями с различной амплитудой (между траекториями с разными радиусами).
А именно, такой механизм увеличивает число траекторий с большими (R>R*) радиусами за счет уменьшения их числа с малыми (R<R*) радиусами.
Величина такого эффекта S
пропорциональна площади фигуры,
ограниченной сверху теоретическими Ро
и снизу экспериментальными Р
распределениями в области R < R*.
Проведенные оценки показывают, что
величина эффекта (
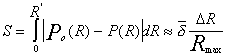 ,где DR-область значений, при которых
DР=Ро-Р>0,
,где DR-область значений, при которых
DР=Ро-Р>0,
Rmax- максимальный радиус,
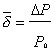 - средняя для
интервала DР амплитуда отклонения
экспериментального распределения от
теоретического) невелика S = (6±2)%
и слабо зависит от частотного состава
анализируемой выборки (табл. 3.3.1).
- средняя для
интервала DР амплитуда отклонения
экспериментального распределения от
теоретического) невелика S = (6±2)%
и слабо зависит от частотного состава
анализируемой выборки (табл. 3.3.1).
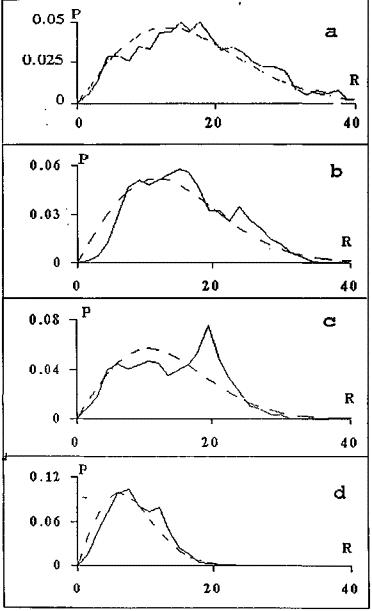
Рис. 3.3.1. Экспериментальные и теоретические (пунктиром) распределения чисел траекторий Р как функции их радиусов R ( в сотых долях угловой секунды), построенные по всей совокупности данных {z} (a), по данным с исключенной годовой гармоникой f1 (b), с исключенными двумя fch,2 и f1 и тремя fch,1, fch,2, f1 (d) гармониками.
Данные, приведенные в таблице 3.3.1, показывают, что максимумы (при R>R*) и минимумы (при R<R*) экспериментальных распределений, значимо отличающие их от соответствующих теоретических распределений, имеют тенденцию группироваться в окрестностях значений, кратных величине: DRw(±dR) »0//,05 » 1,5 м. При этом, величина среднеквадратичного отклонения максимумов и минимумов от центральных значений значительно меньше DRw и, в среднем, составляет dR=0//,01(n=23, dRmin=0, dRmax=0//,025).
Согласно данным работы (Стейси, 1972) такой регулярной составляющей экспериментального распределения Р(R) соответствует вполне определенное изменение величины количества момента инерции ЗемлиDI = (С - А)/DRw и, следовательно, энергии ее вращения DW = 1/2D(IW2) = 1/2W2DI » 1020 дж. Значение DW, по порядку величины близко тектонической (сеймотектонической) энергии ЕST = hES, где, как известно, h » 10-(6¸2) - сейсмический коэффициент полезного действия (seismic efficiency), ES » 1016¸18 Дж – сейсми-
ческая энергия, сбрасываемая в очагах сильнейших (М » 8) землетрясений.
Нам представляется, что совпадение значений таких величин энергий не является случайным. Близость значения DW, определяющего величину энергии «перехода» полюса с одной «регулярной» траектории на другую, значению ЕST = hES, соответствующему энергии, выделяемой при сильнейших землетрясениях, указывает на то, что в рамках развиваемой нами ротационной модели сильнейшие землетрясения могут рассматриваться как определенные «кванты» энергии, соответствующие «регулярным» изменениям режима вращения планеты.
Выше из «возмущенного» уравнения СГ (3.1.1) для скорости поворотной деформации было получено такое решение, которое, по сути, соответствует неустойчивости процесса передачи (перераспределения) поворотной деформации или выделению накопленной упругой энергии.
Следует отметить, что в ротационную модель не закладывались никакие критические условия (критерии) разрушения вещества. Поэтому существование неустойчивости в процессе передачи (перераспределении) поворотной деформации в системе взаимодействующих сейсмофокальных блоков заложено в самой природе сейсмотектонического процесса. Этот вывод является принципиально новым результатом, который предопределен постановкой задачи и ее решением. Как видим, полученный нами новый результат есть прямое следствие постановки задачи о сейсмическом процессе как задачи статистической, изучающей закономерности распределения большой совокупности сейсмофокальных блоков в их взаимодействии друг с другом. Физика такого процесса, как нам представляется, может заключаться в следующем (Викулин, Быков, Лунева, Иванчин, 2000).
Обратная задача для объемного очага землетрясения, как известно, имеет не единственное решение (Павлов, 1996). В работе (Ivanchin, 1994) показано, что для уединенного источника расширения задача (2.4.3)-(2.4.4) имеет два решения U*1~ r-2, U*2 ~ f(J)r-2. Следовательно, общее решение задачи (2.4.3)-(2.4.4) можно записать в виде T = C*1U*1 + C*2U*2, где С*1 и С*2 - произвольные константы, значение которых следует находить не из граничных, а из дополнительных условий. В задаче об уединенном источнике кручения (в рассмотренной выше «ротационной» задаче) два независимых решения, очевидно, будут иметь следующий вид U1~ f(j)r-2, U2 ~ f(J)r-2. При этом «энергетические» свойства решения U1 близки свойствам решения U*1 и общее решение задачи об уединенном очаге землетрясения запишется в виде: T = C1U1 + C2U2. Существование двух решений, в принципе, указывает на наличие и двух значений энергии W1,2, W1 ¹ W2 (энергетических уровней), каждое из которых определяет устойчивое состояние системы.
Как видим, из самых общих соображений следует, что задача об уединенном ротационном очаге имеет (как минимум) два независимых решения. Следовательно, очаг и окружающая его среда могут находиться на двух энергетических уровнях, каждый из которых соответствует квазиравновесному состоянию. Перечисленные выше результаты, вытекающие из анализа решений задачи об уединенном ротационном очаге, позволяют предположить, что неустойчивое решение для скорости поворотной деформации, полученное из «возмущенного» уравнения синус-Гордона (3.1.1), описывает переход блока из одного квазиравновесного состояние в другое с выделением (или, возможно, поглощением) упругой энергии.
Для получения точного решения, описывающего такой переход, очевидно, необходимо решить динамическую задачу о ротационном очаге.
Проведем некоторые оценки с помощью
статической теории (Ivanchin, 1994). Изменение
объема среды для общего решения задачи
упругого равновесия о точечном источнике
расширения дается соотношением DV(T) =
![]() = 2p(2C1 - C2(a + 3)/3). Откуда
следует, что при DV=0 поле диполя сосредоточенной
силы должно определяться соотношением 2С1
- С2(а + 3)/3 = 0 и, следовательно, одна из
констант выражается через другую следующим
образом: С1 = С2(а + 3)/6.
= 2p(2C1 - C2(a + 3)/3). Откуда
следует, что при DV=0 поле диполя сосредоточенной
силы должно определяться соотношением 2С1
- С2(а + 3)/3 = 0 и, следовательно, одна из
констант выражается через другую следующим
образом: С1 = С2(а + 3)/6.
Объемные напряжения, являющиеся следом тензора напряжений, записываются следующим образом S = srr + sjj + sJJ = a r-3 K (3sin2J - 2), где K - коэффициент объемного расширения. Максимальное значение этого выражения достигается на поверхности очага (r = R0) в точке J = ±p/2 и при критерии (критическом условии) разрушения, равном энергетической прочности sЕ (или объемной прочности) (Артамонов, 1976), будет составлять: aC2KR0-3 = sE или С2 = asEKR03. Откуда значение второго коэффициента в случае выделения упругой энергии из объема (о) будет равно:
С1(о) = R03sE(a + 3) /6aK. (3.3.1)
Сдвиговая компонента напряжений равна srJ = C2G(4a - 3)sin(2J)/4r3 . Откуда в случае критерия сдвигового (сд) разрушения значение коэффициента С2 будет равно С2 = 4R03sсд/G(4a - 3) и, следовательно:
С1(сд) = 4(a + 3)R03sсд/6G(4a - 3). (3.3.2)
Как видим, уровни, соответствующие объемным (3.3.1) и сдвиговым (3.3.2) критериям (критическим условиям) выделения упругой энергии, могут значительно различаться. В частности, в задаче об уединенном точечном источнике смещения, по сути близкой задаче о ротационном очаге землетрясения, отношение значений, соответствующих этим энергетическим уровням при средних параметрах, составляет величину около 0,7 (Ivanchin, 1994). При этом уровень «дилатационной» (или, в случае нашей задачи, ротационной) компоненты примерно на 1/3 превышает уровень второй компоненты. Проведенные оценки показывают, что выделение упругой энергии в том или ином конкретном случае может происходить с помощью различных («объемного» или «сдвигового») механизмов.
Таким образом, в результате рассмотрения ансамбля взаимодействующих очагов землетрясений был получен принципиально новый результат. Вещество литосферы, в котором накапливается упругая энергия, может находиться в двух квазиравновесных состояниях, которые определяются самой природой тектонического процесса. Выделение же упругой энергии при сильнейшем землетрясении, т.е. переход вещества, окружающего очаг землетрясения, из одного состояния в другое, осуществляется с помощью механизма, который определяется величиной скорости вращения планеты, ее вариациями и значениями параметров a и m, характеризующих трение и неоднородность вращения сейсмофокальных блоков. Механизмы выделения упругой энергии в физике прочности принято обозначать с помощью соответствующих критических условий: энергия либо выделяется из объема либо «снимается» с поверхности образующейся при землетрясении трещины или системы трещин.
Следует отметить, что механизм диполя сосредоточенной силы в рамках задачи о ротационном очаге не является единственно возможным. Например, в случае, если изменение величины упругих деформаций приводит к изменению объема (что, например, происходит при деформировании твердых тел с инородными включениями), то есть при DV ¹ 0, то может быть реализован дилатационный механизм напряженного состояния. Это означает, что механизм диполя сосредоточенной силы не является единственным и при некоторых условиях даже преобладающим. В этом случае, вследствие появления новых квазиравновестных энергетических уровней, число которых в случае n очагов может составить 2n, решение задачи становится неоднозначным, что происходит вследствие невозможности определить некоторые из констант Сi ввиду недостаточного для этого количества физических условий.
Оптимизм 60-70-х годов прошлого века относительно возможности решить проблему прогноза землетрясений сменился в конце 80-х-начале 90-х годов глубоким пессимизмом. Почему это произошло?
К концу 60-х годов уже были разработаны теоретические модели землетрясения: теория лавинно-неустойчивого трещиннобразования - в нашей стране (Мячкин, Костров, Соболев, Шамина, 1971; Брейс, Мячкин, Дитрих, Соболев, 1976) и теория дилатансии - за рубежом (Nur, 1972; Sholz, Sykes, Aggarwal, 1973). Они описывали основные стороны процесса и давали качественное объяснение большинству известных предвестников землетрясений. Казалось бы, для надежного предсказания землетрясений осталось решить чисто технические задачи: повысить плотность сейсмических станций и оснастить их хорошими приборами. При этом предполагалось получить «количественную» привязку предвестников к конкретным землетрясениям.
Однако эксперименты, проведенные как у нас, так и на зарубежных сейсмологических полигонах, показали, что распределение предвестников представляет собой мозаичную картину. Иными словами, увеличение плотности наблюдательной сети (повышение точности наблюдений) привело не к локализации предвестников в пространстве и во времени, а к «размыванию» их множества.
Полученный результат имеет, на наш взгляд, фундаментальное значение. Предвестники существуют - это факт. Но связаны они не с конкретными землетрясениями, как предполагалось, а с их совокупностями, т.е. с некоторым общим геофизическим процессом, только иногда завершающимся землетрясениями.
Выше нами была предложена концепция построения такого процесса, в рамках которой удалось «слить» идею С.А.Федотова (1965, 1968) о тенденции к непересечению очагов сильнейших землетрясений с представлениями о миграции сейсмичности и, тем самым, привнести в долгосрочный прогноз временной аспект - предсказание времени сильнейших землетрясений (Викулин, 1989, 1990, 1992). Соответствующие прогнозные схемы, разработанные в рамках такого подхода, представлены выше.
По-видимому, впервые на глобальном уровне такое слияние пытался осуществить К.Моги в 60-х годах прошлого века. Однако довести эту идею до конца ему так и не удалось. Причина, по-видимому, заключена в том, что в то время отсутствовали физические модели, в рамках которых можно было бы пытаться объяснить процессы миграции, протекающие на планетарном уровне (Elsasser, 1969; Savage, 1971; Лобковский, Баранов, 1984; Николаевский, 1996). Принципиальная возможность долговременного прогноза, как полагает автор работы (Hagivaka, 1969), была продемонстрирована в 1965-1966 гг. на примере землетрясения в Мацусиро (Япония).
Описанные выше результаты, полученные в настоящей работе, позволяют подойти к проблеме прогноза землетрясений с других позиций.
В рамках волновой ротационной модели аналитическими методами выявлена особенность, отвечающая неустойчивому характеру движения сейсмофокальных блоков при их взаимодействии с тектоническими волнами. Согласно данным лабораторных исследований, по сути, такую же неустойчивость должно иметь поле напряжений в очаге землетрясения во временной окрестности главного толчка, включающей его форшоковую и афтершоковую стадии. Другими словами, существование возможности количественного описания фор-афтершоковой стадии сейсмического цикла численными методами, в принципе, позволяет построить такую теорию прогноза сильнейших землетрясений, включающей указание и времен толчков, и мест расположения их очагов, которая, по сути, является в большей степени детерминированной, чем статистической. Как видим, ротационная модель сейсмического процесса открывает новые пути решения проблемы прогноза землетрясений. Для ее решения «центр тяжести» исследований физики процесса необходимо в дальнейшем переносить с очага отдельно взятого землетрясения на совокупность очагов.
Из заложенных в основу ротационной модели двух параметров - размера сейсмофокального блока R0 или соответствующего ему волнового числа k0 (2.4.29, 2.4.37) и скорости миграции с0 (2.4.30, 2.4.38), можно определить характерный для сейсмического процесса временной интервал
Т = (сk0)-1 ~ (R0/WVS)1/2 (3.4.1)
продолжительность которого не зависит от плотности выделяемой сейсмической энергии в регионе (2.4.33) и определяется только значением характерного размера слагающих его блоков или очагов сильных землетрясний R0. Видимо, этим и можно объяснить тот факт, что сейсмические периоды одинаковой продолжительности были выделены для практически всех достаточно активных регионов планеты (раздел 2.2). Этот результат позволяет ротационную модель применять к расчету параметров сейсмического процесса, протекающего в пределах любого сейсмоактивного региона, не зависимо от уровня его сейсмической активности.
Полагая протяженности очагов землетрясений (L » 2R0) связанными с их магнитудами соотношением, установленным в работе (Ризниченко, 1976), которое, как можно видеть из графиков на рис. 1.1.2, в диапазоне М ³ 7 практически совпадает с полученным нами для курило-камчатской и японской островных дуг выражением, из (3.4.1) для продолжительности характерного для сейсмического процесса временного интервала получим следующее соотношение:
lg T » (0,2±0,1)×M + A (3.4.2)
где А = A(W,r,G) - константа.
Можно построить цепочку логических рассуждений, из которой будет следовать, что полученные в настоящей работе данные и их интерпретация, т.е. «привязка» к имеющим место закономерностям сейсмичности, позволяют провести параллель между значением Т, определяемым соотношением (3.4.2), и временем предвестника землетрясения.
Анализу предвестников землетрясений посвящено большое количество работ. Отметим лишь некоторые из них (Niazi, 1984-1985; Зубков, 1987; Сидорин, 1992; Рикитаке, 1979). Соотношение для времени предвестника, построенное в работе (Ананьин, 1977) по комплексу данных о землетрясениях Кавказа, близко соотношению (3.4.2).
В работе (Соболев, 1993) со ссылками на большое количество авторов, в том числе и на цитируемые выше работы, приведен обширный материал о значениях коэффициентов, определяющих ход графика lgT=aM-b: наклон «а», свободный член «b» и коэффициент корреляции «r», для каждого из предвестников в отдельности. Из данных этой работы следует, что соотношению (3.4.2) наилучшим образом соответствуют наклоны графиков, построенных для следующих среднесрочных (месяцы-годы) предвестников: земные токи (а=0,18, r = 0,91), уровень и дебит источников подземных вод (а=0,23-0,34, r=0,79-0,91), электросопротивление (а=0,30, r=0,89). При уровне корреляции r ³ 0,6 среди краткосрочных (дни - часы) предвестников можно выделить следующие: атмосферное электричество (а=0,33, r=0,62) и деформации (а=0,36, r=0,60). Согласно данным работы (Соболев, 1993) другие предвестники характеризуются либо большими значениями наклонов «а» при высоких «r», либо значениями наклонов а=0,2±0,1, но с низкими коэффициентами корреляции r £ 0,5-0,6.
Следует отметить, что в соответствии с накопленными на Камчатке материалом все отмеченные нами выше предвестники - электромагнитные (земные токи, электросопротивление и атмосферное электричество), уровень и дебит источников подземных вод и деформационные - имеют так называемый «бухтообразный» характер.
Совпадение значений наклонов «теоретического» графика (3.4.2), с одной стороны, и экспериментальных графиков для выделенной нами группы предвестников - с другой, представляется неслучайным. Такое совпадение, по-видимому, является отражением волнового тектонического характера сейсмического процесса, имеющего блоково-солитонное строение. В рамках таких представлений, бухтообразный характер предвестников становится понятным: это есть проявление взаимодействия сейсмофокальных блоков и тектонических волн друг с другом, наблюдаемое в различных геофизических полях.
©IVGG 2003