Существует две противоположные точки зрения на периодичность сейсмического процесса. С одной стороны, анализ особенностей пространственного и временного распределения землетрясений совершенно определенно указывает на существование характерных сейсмических периодов. Так, выше в разделе 1.1, для класса сильнейших сейсмических событий - как особенности взаимного распределений афтершоковых областей землетрясений в пространстве, показано существование двух характерных для сейсмического процесса временных интервалов: сейсмического цикла Тс (1.1.2) и повторяемости Тr (1.1.3). Анализ региональных каталогов, каждый из которых содержит достаточно полный список землетрясений за достаточно продолжительный отрезок времени, как правило, приводит к появлению и более длинных (значительно больше Тr,c) периодов (Мушкетов, Орлов, 1893; Davison, 1936; Kawasumi, 1951; Кириллова, 1957; Мэй Шиюн, 1960; Тамразян, 1962; Федотов, 1965; Филлипас, 1965; Ambraseys, 1970; Shimazaki, Nakata, 1980).
С другой стороны, анализ большого количества исследований по повторяемости землетрясений, проведенный в работах (Aki, 1956; Lomnitz, 1966,1974), позволил установить существование большого количества периодов, значения которых лежат в широком диапазоне от минут до многих сотен и, по-видимому, первых тысяч лет. На основании этих данных в работе (Рикитаке, 1979) делается вывод о том, что «если бы все эти периодичности действительно существовали, в результате получился бы почти белый шум». Откуда следует, что сейсмический процесс не является периодическим.
Общепринятая методика исследования распределения землетрясений по интервалам между ними сводится к следующему. На первом этапе исследования, путем фиксации границ магнитудного диапазона и пространственно-временной области, формируется совокупность землетрясений. На втором этапе составляется числовая последовательность, количественно характеризующая распределение следующих друг за другом землетрясений по интервалам между ними (экспериментальная последовательность). На третьем этапе для анализируемой совокупности землетрясений проводится расчет теоретической числовой последовательности, соответствующей тому или иному известному закону распределения, обычно, закону Пуассона. На четвертом этапе экспериментальная и теоретическая последовательности сравниваются между собою. Результат сравнения количественно выражается соответствующим значением доверительной вероятности Р. При этом полагают, что некая закономерность в распределении землетрясений во времени существует в том случае, если значение Р превышает некоторую критическую величину Ркр, которая задается из априорных соображений.
В каждом исследовании оценка статистической значимости, как правило, проводилась для одного распределения, которое на плоскости магнитуда М - время t характеризуется одной точкой с координатами М0 и t0, где М0 фиксирует (обычно снизу, М ³ М0) значение магнитуд исследуемой совокупности землетрясений, t0 - продолжительность периода, статистическая значимость которого для такой совокупности устанавливается.
Применение такой методики, как показано выше, приводит к парадоксальному результату, который заключается в том, что для отдельных совокупностей землетрясений закономерности существуют, в то время как для всей совокупности землетрясений они отсутствуют.
Приведенные в разделе 1.1 данные показывают, что некоторые периодичности (или квазипериодичности, т.е. почти периодичности) все же реальны. На это указывает высокое значение оправдываемости долгосрочного сейсмического прогноза, в основе которого как раз и заложены представления о цикличности сейсмического процесса. Поэтому наиболее вероятная причина такой неоднозначности заключается в существовании определенного произвола при формировании исходной выборки статистических данных. Интуитивно ясно, что на основании существующих каталогов землетрясений всегда (или практически всегда) можно так сформировать исходные данные (в разумных пределах варьируя пространственными координатами гипоцентров и магнитудами землетрясений с учетом реальной точности определения их значений), чтобы и выборка была статистически значимой, и расчетное значение соответствующей доверительной вероятности было достаточно высоким.
Как видим, противоречивость вывода о периодичности сейсмического процесса, скорее всего, является следствием не достаточно корректного формирования исходных совокупностей землетрясений. В результате чего при проведении вычислений, обосновывающих статистическую значимость сейсмических периодов, в некоторых случаях были получены завышенные значения соответствующих доверительных вероятностей, что в результате и привело к появлению «мнимых» периодов и, как следствие, к выводу о «белом сейсмическом шуме».
Формирование совокупностей данных, кроме того, необходимо проводить с учетом условий, которые накладываются эффектами группирования землетрясений. Действительно, существование классов землетрясений (см., например, разделы 1.1 и 1.3) допускает наличие у всех событий одного класса, т.е. землетрясений определенного магнитудного диапазона М ³ М0, тождественных свойств. Физически это означает, что в случае выявления какой-либо закономерности для совокупности землетрясений с М ³ М1, М1 ³ М0, появление такой же закономерности следует ожидать и для другой совокупности землетрясений с М ³ М2, М2 ³ М0, М2 ¹ М1. Другими словами, статистическое исследование должно опираться на такой способ формирования совокупностей землетрясений, который является методически корректным в широком диапазоне магнитуд.
В свете сказанного представляется, что при статистических исследованиях для корректного выявления закономерностей распределения землетрясений во времени методику исследования необходимо изменить следующим образом. Все промежуточные совокупности данных должны формироваться на основании одной «генеральной» выборки, составление которой должно быть проведено с использованием максимально полного объема известных данных. Такой подход к формированию генеральной выборки, в свою очередь, позволит в широком диапазоне магнитуд и продолжительностей интервалов: М1 £ М0 £ М2, t1 £ t0 £ t2 обеспечить достаточно корректный переход от «точечного» анализа к анализу значений доверительной вероятности Р на плоскости М0 - t0. Кроме того, для сравнения, параллельно с анализом «кумулятивных» совокупностей с М ³ М0 представляется целесообразным анализировать и статистически от них независимые «дискретные» совокупности с М=М0.
При этом, методика расчета значений доверительной вероятности в каждой точке М0, t0 плоскости М0-t0 остается прежней; она включает описанные выше четыре этапа. В качестве теоретического в расчетах будем использовать распределение Пуассона. Сравнение экспериментальных и теоретических распределений будем проводить с использованием критерия c2.
При статистических исследованиях систем, состоящих из достаточно большого количества объектов, как известно (Ландау, Лифшиц, 1964), «появляются новые своеобразные закономерности», которые «ни в какой степени не могут быть сведены к чисто механическим закономерностям. Их специфичность проявляется в том, что они теряют всякое содержание при переходе к механическим системам с небольшим числом степеней свободы». Именно поэтому для исследования таких статистических систем разработана специальная концепция, получившая название фазового пространства. Каждая точка такого пространства соответствует определенному состоянию анализируемой системы. Таким образом, исследование состояния статистической системы сводится к анализу траекторий движения точек в фазовом пространстве. Закономерное распределение точек в фазовом пространстве описывается функцией статистического распределения, которая имеет вероятностную природу.
Как видим, в случае, если на плоскости М0-t значения доверительной вероятности Р распределены в соответствии с какими-либо закономерностями, то эти закономерности могут быть проинтерпретированы в рамках физически обоснованной концепции.
Возможность применения к сейсмостатистическим задачам принципов статистической физики в будущем может оказаться достаточно плодотворной. На настоящем уровне исследований, как представляется, практическое применение этих принципов является скорее физически правдоподобным, чем строго обоснованным.
Использование статфизического подхода, в частности, достаточно наглядно позволяет обосновать статистическую независимость разных достаточно больших по размеру сейсмических подсистем. Скажем, процессы, протекающие в пределах разных островных дуг в течение непродолжительного отрезка времени Т1 (меньшего некого характерного интервала Т0, Т1 < Т0), могут рассматриваться как статистически независимые друг от друга. Тогда, объединяя сейсмостатистические данные по n островным дугам в одну выборку, получаем эффективный ряд наблюдений для этой выборки продолжительностью Тэфф = nT1.
Инструментальные данные о достаточно сильных (М ³ 7) землетрясениях имеются за период времени продолжительностью около 100 лет, в то время как продолжительность сейсмического цикла, как показано в разделе 1.1, составляет Тс » 200 лет. Поэтому используя данные инструментальных наблюдений для нескольких островных дуг, в рамках предложенного сейсмостатистического подхода оказывается возможным выявлять сейсмические периоды продолжительностью Тс и более.
Возможность достаточно убедительного обоснования двух взаимоисключающих точек зрения на проблему периодичности сейсмического процесса (Рикитаке, 1979) указывает на существование определенного произвола при формировании выборки данных при сейсмостатистических исследованиях закономерностей распределения землетрясений во времени (Викулин, 1984, 1988). Одним из возможных объективных методов, с помощью которого можно было бы проверить достоверность той или иной закономерности, выявленной методами математической статистики, является способ, опирающийся на концепцию фазового пространства. В рамках такой концепции, например, наличие или отсутствие периодичности однозначно определяется соответственно существованием или отсутствием в таком пространстве замкнутой фазовой траектории.
Применение такого подхода к задачам сейсмологии было обосновано в работах (Викулин, 1984, 1988, 1990). В его основе заложен анализ двухмерного поля значений доверительной вероятности Р(М, t), которые служат мерой отличия реальных распределений землетрясений по временным интервалам между ними от теоретических распределений Пуассона в широком диапазоне магнитуд М1 £ М £ М2 и продолжительностей временных интервалов t1 £ t £ t2. Основные методические моменты анализа приведены выше.
Проводился сравнительный анализ двух совокупностей событий, которые были представлены выборками землетрясений с М ³ М0 и с М = М0, названных кумулятивными и дискретными соответственно. Для каждой выборки исследование проводилось на двух уровнях. На первом в качестве исходного материала использовались инструментальные каталоги северо-западно-тихоокеанских землетрясений с М ³ 7, Н < 100 км, происшедших в ХХ столетии. Всего таких землетрясений в 1904-1980 гг. произошло 264, из них 75 - в пределах сейсмофокальной зоны алеутской дуги, 95 - курило-камчатской, включая о. Хоккайдо, и 94 - о. Хонсю. Использование данных трех островных дуг, представленных 100 летним периодом наблюдений, позволяет, как представляется, выявлять периодичности с продолжительностью до 300 лет.
На втором уровне использовались данные детальных сейсмологических наблюдений о землетрясениях энергетических классов 10 £ К £ 14¸15 (3 £ М £ 7), происшедших в 1958-1980 гг. в очагах сильнейших курило-камчатских событий. Общее число анализируемых землетрясений такого магнитудного диапазона составило многие сотни. Как видим, исходные сейсмологические данные являются статистически достаточно представительными.
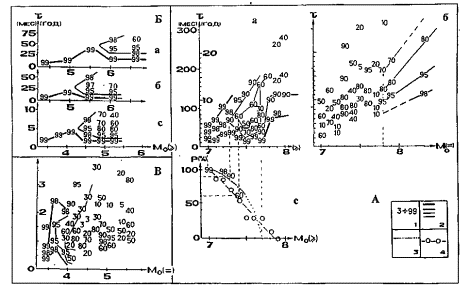
Результаты расчетов приведены на рис. 2.2.1. Из данных, представленных на этом рисунке, видно, что в случае обеих совокупностей землетрясений - кумулятивных с М ³ М0 (³) и дискретных с М = М0 (=), значения доверительной вероятности в диапазонах малых 3 £ М0 £ М01 = 4,5-5,0 и больших М0 ³ М02 = 7,7 магнитуд распределены явно не случайным образом. А именно, одинаковые значения доверительной вероятности располагаются вдоль линий (изолиний), которые не пересекают друг друга (рис. 2.2.1 Аа, Аб, Б, В).
Ниже установим закономерности сейсмического процесса, соответствующие такому расположению точек Р. Здесь подчеркнем следующее. Кумулятивные и дискретные совокупности можно считать статистически независимыми. Поэтому магнитуды М01 и М02, по сути, являются особыми точками временного (t) распределения:
Мt1 = 4,5 - 5,0 , (2.2.1)
Мt2 = 7,7 , (2.2.2)
так как в небольших окрестностях этих точек закономерности сейсмического процесса, соответствующие изолиниям доверительной вероятности и их особенностям, могут изменяться достаточно сильно.
Как видно из данных, представленных на рис. 2.2.1 Аа, каждая изолиния кумулятивного распределения может быть апроксимирована тремя прямолинейными отрезками, «горизонтальным» (t = const), в центре, и двумя «наклонными». При этом, длины горизонтальных отрезков пропорциональны значению доверительной вероятности DМ0 = Mt2 - M0 ~ Р и определяются положениями их левых концов, поскольку положение правых, не зависимо от Р, фиксировано особым значением магнитуды Мt2 (2.2.2).
Графически зависимость, характеризующая протяженность горизонтальных участков изолиний доверительной вероятности как функция Р, в виде сплошной линии, продолжающейся точками, представлена на рис. 2.2.1 Ас. Пустыми кружками и пунктирной линией на этом же рисунке изображен график, характеризующий долю японских, курило-камчатских и алеутских землетрясений 1904-1982 гг. с М ³ Мt2 = 7,7 , имеющих форшоки и афтершоки первого года с М ³ М0. Данные о сильных (М ³ 6) форшоках и сильнейших курило-камчатских и японских землерясений ХХ века приведены в Приложении 1. Под форшоками и афтершоками, как и выше, в соответствии с (Соболев, 1993), понимаются землетрясения, эпицентры которых попадают внутрь очаговых областей землетрясений с М ³ Мt2, границы которых изображены на рис. 1.1.1. Из данных, представленных на рис. 2.2.1 Ас, видно, что обе зависимости являются достаточно близкими. Следовательно, землетрясения магнитудного диапазона 7 £ М £ Мt2 = 7,7, по сути, являются сильными (см. раздел 1.3) форшоками и афтершоками землетрясений с М ³ Мt2 = 7,7. Нижней границей такого класса событий, как можно предположить на основании данных, представленных на рис. 2.2.1 Аа, Б, является особое значение магнитуды Мt1 = 4,5-5,0.

Рис. 2.2.1. Характеристика «кумулятивных» (³) (А. а; Б) и «дискретных» (=) (А, б; В) распределений чисел землетрясений по временным интервалам между ними на двух уровнях: А – северо-западная часть Тихого океана, М ³ 7, 1904 – 1980 гг. и Б, В – очаги курило-камчатских сильнейших знемлетрясений, К ³ 10 (М ³ 3): Итурупское 6.11.1958, М = 8,2, афтершоковая стадия (Б, а); Урупское 13.10.1963, М = 8,0 , форшоковая стадия (Б, б) и Большое Камчатское 4.11.1952, М = 8,5, стадия стабилизации (Б, с). 1, 2 – значения доверительной вероятности Р и соответствующие им изолинии, «толщина» которых пропорциональна Р; 3 – график зависимости, характеризующей долю сильнейших землетрясений, имеющих форшоки и афтершоки первого года с М ³ М0; 4 – график зависимости, характеризующей протяженность горизонтального участка изолинии доверительной вероятности.
Таким образом, показано, что длины горизонтальных отрезков изолиний пропорциональны значению доверительной вероятности Р: DМ0 = Mt2 - M0 ~ P и определяют долю сильнейших землетрясений, имеющих форшоки и афтершоки с М ³ М0. Тем самым дана интерпретация введенной выше величины доверительной вероятности и показано, что землетрясения магнитудного диапазона Мt1 £ M £ Mt2 являются сильными фор-афтершоками.
Рассмотрим всю совокупность изолиний на кумулятивной плоскости М0(³)-t. Как видно из данных, представленных на рис. 2.2.1 Аа, изолинии доверительной вероятности, не пересекаясь между собою, при Р ® 60% «непрерывно» стягиваются к замкнутой линии. Физика замкнутой линии на фазовой плоскости, как известно, заключается в том, что соответствующий этой линии процесс является периодическим. Определим продолжительность периода. Для этого, записывая математическое выражение для изолинии в виде Р(М0, t) = const, дифференцируя его, получаем, вследствие непересечения изолиний, уравнение:
![]() ,
,
которое тождественно выполняется вдоль «горизонтальных» (т.к. ¶Р/¶М0=0, Dt=0) и правых «вертикальных» (т.к. ¶Р/¶t=0, DМ0=0) прямолинейных отрезков изолиний. Следовательно, величина периода волнового движения, отражением которого на фазовой плоскости М0(³)-t является замкнутая изолиния, будет равна длине ее горизонтального участка DМ0, умноженной на наклон левого (l) прямолинейного отрезка изолинии аl=(dt/dM0)l:
Tt = аl×DМ0 .
Cогласно данным, представленным на рис. 2.1.1 Аа, значения этих величин составляют DМ0 = 7,55 ± 0,15 и al » 30±7 год/ед. магнитуды ¹ f(P), откуда для величины сейсмического периода получаем следующую оценку:
Tt = 230 ± 60 лет (2.2.3)
Эта величина близка предельному значению периода, который может быть выявлен в рамках используемой при анализе методики, описанной выше в разделе 2.1. Поэтому полученные данные могут рассматриваться в качестве доказательства лишь квазипериодического (или почти периодического) характера сейсмического процесса. С этим же обстоятельством, возможно, связаны и достаточно низкое значение доверительной вероятности вдоль замкнутой изолинии - Р=60% и большой (около 50%) разброс экспериментальных значений повторяемостей сильнейших тихоокеанских землетрясений (1.1.3). Однако, возможна и другая интерпретация. А именно, периодичность - как закономерность, является характерным (адекватным) свойством сейсмического процесса; значение же периода зависит от ряда «региональных» параметров, что и объясняет большой разброс его значений.
Таким образом, анализ свойств распределения землетрясений во времени выявил существование двух особых значений магнитуд Mt1 и Mt2, которым соответствуют такие две (вообще говоря, взаимосвязанные) особенности сейсмического процесса, как его квазипериодичность и существование класса сильных фор-афтершоков.
Для проверки предположения о «стыковке» данных, представленных на рис. 2.2.1 Аа, Б, т.е. расширении поля значений доверительной вероятности в область меньших магнитуд на рис. 2.2 Аа и в область больших магнитуд на рис. 2.2.1 Б, был проведен анализ особенностей распределения курило-камчатских землетрясений во времени с использованием другой методики (Журавлев, 1982, 1983). Основой этой методики является расчет статистик разностей времен между ближайшими во времени землетрясениями и их сравнение со случайным стационарным потоком Пуассона, в котором вероятность Р появления следующего во времени события через интервал t оценивается соотношением (Рикитаке, 1979):
Р = m×e-mt,
где m-1 - средний временной интервал между землетрясениями, принадлежащими анализируемой совокупности данных. При анализе использовались данные о коровых (Н < 100 км) курило-камчатских землетрясениях 1911-1961 гг. (N » 3000), которые содержатся в каталоге (Викулин, Ким, 1983). Исследовались кумулятивные совокупности землетрясений с М ³ М0, в которых граничная магнитуда принимала следующие значения М0 = 4,8; 5,0; 5,3; 5,8; 6,5 и 7,0.
Гистограммы, характеризующие распределения разных совокупностей землетрясений во времени, представлены на рис. 2.2.2. Видно, что в диапазоне граничных магнитуд 5,3 £ М0 £ 7,0 все экспериментальные гистограммы близки распределению Пуассона в окрестности точки t0 = 45 суток. Значения t1 и t2, t1 < t2, определяющие границы областей, в пределах которых наклоны теоретических и экспериментальных гистограмм являются близкими, определяются достаточно уверенно (на рис. 2.2.2 они отмечены вертикальными стрелками). Как видно из данных, представленных на рис. 2.1.3 а, с изменением граничной магнитуды М0 границы таких областей в окрестности точки t0 изменяются вполне закономерным образом. А именно, при увеличении М0 продолжительность временного интервала, в пределах которого экспериментальные и теоретические распределения близки, увеличивается от нуля при М01 = 5,1 ± 0,3 до своего максимального значения при М02 = 7,7 ± 0,3.
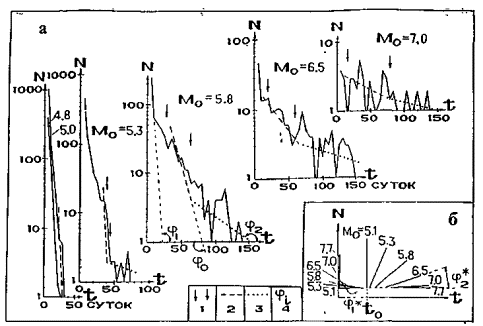
Рис. 2.2.2. Гистораммы, характеризующие статистики разностей времен между ближайшими во времени землетрясениями, построенные для совокупностей курило-камчатских землетрясений 1911–1961 гг. с М ³ М0 в диапазоне М0 = 4,8–7,0 (а), и «синтезированная» по всем данным гистограмма (б). 1 – границы в окрестности точки t0 = 45 суток временных интервалов: значения t1 и t2, t2 > t1, в пределах которых статистики разностей близки распределению Пуассона; 2 – теоретическое распределение Пуассона для каждого М0; 3 – сглаженная гистограмма при t > t2; 4 – углы для разных частей гистограмм, индекс обозначает: i = 0 для t < t1 и i = 2 для t > t2.
При малых (t < t1) временах больший по сравнению с «пуассоновым» наклон левой части экспериментальной гистограммы (j1 < j0), очевидно, объясняется особенностями афтершокового и форшокового процессов - т.е. эффектом, который вследствие высокой частоты появления событий, может быть назван эффектом «притяжения» землетрясений друг к другу. Тогда меньший «пуассонового» наклон правой части гистограммы при t > t2 (j0 < j2), согласно той же логике, должен соответствовать эффекту «отталкивания» землетрясений.
Эффекты притяжения и отталкивания
проявляются на разных «относительных»
временах. На плоскости М0-t (рис. 2.2.3 а)
им соответствуют «фазовые» области,
расположенные ниже прямой t1 (фор-афтершоки)
и выше прямой t2 (эффекты отталкивания).
Тогда на такой плоскости должны
существовать две особые точки, по сути,
критические.
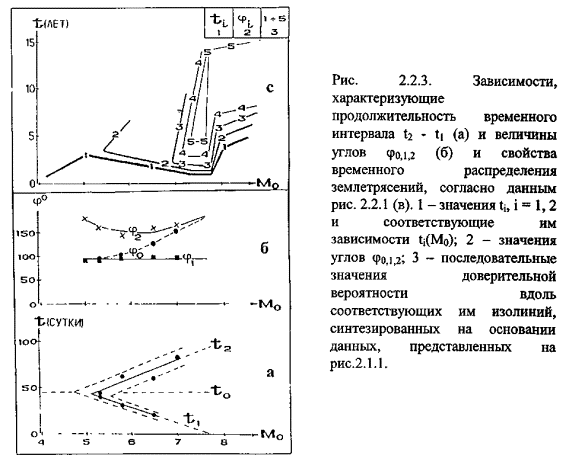
Первая такая точка, в окрестности которой фазы, соответствующие эффектам «притяжния» и «отталкивания», находятся в равновесии друг с другом, расположена на пересечении прямых t1 и t2:
Мtс1 = 5,1 ± 0,3 (2.2.4)
Вторая точка – есть точка пересечения прямой t1 с осью ординат М0:
Мtс2 = 7,7 ± 0,3 (2.2.5)
Таким образом, распределение землетрясений во времени обнаруживает две закономерности, которые могут быть отождествлены с эффектами притяжения и отталкивания. На плоскости М0 - t (рис. 2.2.3 а) этим эффектам соответствуют определенные фазовые области, ограниченные прямыми t1 и t2, и критические точки, расположенные в окрестностях магнитуд Мtc1 и Mtc2. В части плоскости, заключенной между прямыми t1 и t2, в соответствии с используемой здесь «термодинамической» аналогией, допускается существование обеих фаз, которые, «перемешиваясь», тем самым и рождают пуассоновый (случайный) поток событий.
Как видим, имеют место равенства между особыми (2.2.1), (2.2.2) и критическими (2.2.4), (2.2.5) значениями:
Мt1 » Mtc1 (2.2.6)
Mt2 » Mtc2 (2.2.7)
Иными словами, применение другой методики анализа позволило для распределения землетрясений во времени подтвердить как существование двух особых точек, так и значения соответствующих им критических магнитуд.
Следует подчеркнуть, что выявленные в этом разделе особенности являются характерными свойствами только временного распределения землетрясений, т.к. при формировании исходных совокупностей данных никакие ограничения, связанные с теми или иными особенностями других распределений (пространственного, энергетического и др.) землетрясений, при проведенном исследовании не накладывались.
Равенство особых значений соответствующим критическим значениям также указывает на то, что изолинии, представленные на рис. 2.2.1 Аа, Б, действительно могут быть состыкованы друг с другом (рис. 2.2.3 б, в). Таким образом, в рамках разрабатываемого в настоящей работе подхода сейсмический процесс может быть представлен как набор всех возможных состояний, которые реализуются в классе сильных (фор-афтершоков и сильнейших) землетрясений в течение характерного периода (сейсмического цикла).
Тем самым было показано, что закономерности распределения значений доверительной вероятности Р на (кумулятивных и дискретных) плоскостях магнитуда - время отражают особенности сейсмического процесса. Поэтому представляется, что такие плоскости и (или) их аналоги могут считаться фазовыми и в дальнейшем использоваться для построения статистической физики (термодинамики) сейсмического процесса.
Близость значений граничных магнитуд, «отсекающих» классы сильнейших землетрясений по особенностям пространственного Мsp (1.1.1) и временного Мt2 (2.2.1) распределений,
Мsp =7,7±0,2 » Мt2 = 7,7 = MST (2.3.1)
указывает на то, что класс сильнейших событий является в то же время и такой группой землетрясений, очаги которых закономерным образом распределены в пространстве-времени. Данные, приведенные на рис. 2.3.1, показывают, что очаги сильнейших северо-западно-тихоокеанских землетрясений группируются в цепочки, в пределах которых они мигрируют в направлении с юго-запада на северо-восток со скоростью равной
V = 250 ± 30 км/год (2.3.2)
Близкие значения скоростей миграции и то же ее направление вдоль окраины Тихого океана в классе достаточно сильных землетрясений (М ³ М0 , где, в зависимости от региона, 7,5 £ М0 £ 8,3) независимо от наших данных были получены другими авторами (Mogi, 1968; Вилькович, Шнирман, 1982; Касахара, 1985). Такие совпадения как в исходных данных (значение М0 близко установленным нами особым магнитудам Мsp и Мt, «отсекающим» класс сильнейших землетрясений), так и в полученных результатах (совпадение значений скоростей миграции при том же ее направлении), подтверждают сформулированный нами выше вывод о том, что миграция сильнейших землетрясений является пространственно-временной закономерностью сейсмического процесса.
На рис. 1.1.3 представлены очаги сильнейших (М ³7,9) нанкайских землетрясений 684-1946 гг., границы которых по макросейсмическим данным (Омори, 1913; Соловьев, Го, 1974) были определены нами. Из данных, представленных на этом рисунке, видно, что весь район разбивается на три зоны примерно равной протяженности – центральную, расположенную между продолжениями полуостровов Кии и Идзу, и две боковые. Период повторяемости сильнейших землетрясений в пределах каждой зоны примерно одинаков (130±40 лет, табл. 1.1.1) и близок среднему периоду повторения для окраины Тихого океана (100±50 лет, соотношение 1.1.3). При этом имеет место миграция очагов двух видов. «Продольная» миграция наблюдается из одной зоны в другую в направлении с северо-востока на юго-запад с интервалом, протяженность которого изменяется от нуля («дуплет» землетрясений 28.Х.1707 г.) до 23 лет (цепочка событий 1.9.1923 - 7.12.1944 - 21.12.1946). «Поперечная» миграция имеет место в пределах каждой зоны в сторону береговой линии со скоростью
VN^ = 0,2 км/год (2.3.3)
при характерном времени миграции порядка
ТN^ = 600 лет (2.3.4)
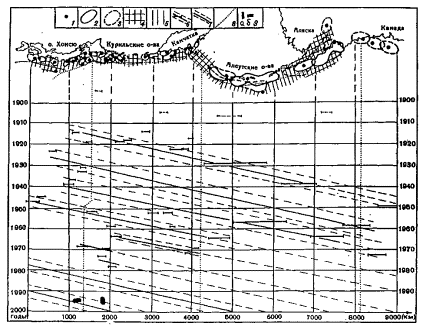
Рис. 2.3.1. Пространственно – временная карта очаговых областей северо–западно-тихоокеанских сильнейших землетрясений 1904-1986 гг. 1 - эпицентры землетрясений; 2, 3 - соответственно уверенные (и менее уверенные) и вероятные границы очаговых областей землетрясений, представленные на рис. 1.1.1; 4 - наиболее вероятные места, в пределах которых в будущем могут располагаться очаговые области сильнейших землетрясений; 5 - менее вероятные места расположения очаговых областей таких же землетрясений; 6 - положение очаговых областей землетрясений на пространственно-временной карте и проведенные по ним миграционные цепочки; 7 - прогнозные цепочки, в пределах которых в будущем следует ожидать появление очаговых областей сильнейших землетрясений (Викулин, 1989, 1990); 8 - оси глубоководных желобов; 9 – сильнейшие землетрясения: Шикотанское 4.10.1994, М = 8 (а) и вблизи о. Хонсю 28.12.1994, М = 7,9 (б).
На рис. 2.3.2 представлены очаги сильнейших (М ³ 7,6) землетрясений 1737–1971 гг., очаги которых определены в работах (Федотов и др., 1980; Викулин, 1987, 1988). Из данных, представленных на этом рисунке видно, что при повторяемости сильнейших землетрясений в одном блоке, близкой повторяемости в пределах Тихого океана, как и в случае желоба Нанкай, выделяется миграция двух видов – продольная и поперечная. При этом наблюдаются два типа продольной миграции: первого типа - с юго-запада на северо-восток при продолжительности цепочки от нуля до 26 лет и второго типа (встречная миграция) - в обоих направлениях вдоль зоны со скоростью
V = 4 ± 1 км/год (2.3.5)
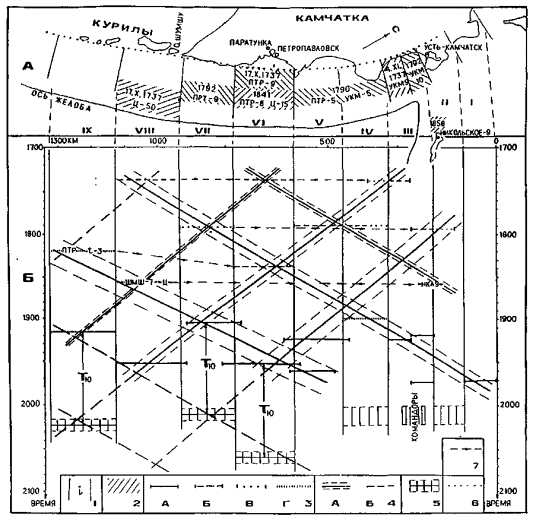
Рис. 2.3.2. Расположение очагов сильнейших северо–курильских и камчатских землетрясений XVШ-XIX вв. в пространстве (А) и таких же землетрясений XVII-XX вв. в пространстве-времени (Б). 1 – границы блоков сейсмофокальной зоны; 2 – вероятное положение очаговых областей землетрясений XVII-XIX вв.; цыфры обозначают: год землетрясения, балльность по шкале MSK-64 в Петропавловске–Камчатском (ПТР), Усть-Камчатске (УКМ), Никольском (НКЛ) и на о. Шумшу (ШМШ); высоту волны цунами и t = 3 – длительность отмеченных при землетрясени колебаний, мин.; 3 – положение очаговых областей землетрясений в ХХ в. на пространстывенно – временной карте (а); достаточно уверенное (б), менее уверенное (в) и вероятное (г) положение очаговых областей землетрясений XVIII-XIX вв. на пространственно - временной карте; 4 – цепочки очаговых областей землетрясений XVIII-XX вв., мигрирующих вдоль зоны со скоростью 4±1 км/год (а) и теоретическое продолжение таких цепочек в будущее (б); 5 - пространственно-временные области, в пределах которых должны располагаться очаговые области землетрясений в будущем; 6 – западная граница сейсмофокальной зоны (Гусев, Шумилина, 1976); 7 – цепочки очаговых областей XVII-XIX вв. землетрясений, мигрирующих в северо-восточном направлении; Тю = 108 ± 7 лет – повторяемость сильнейших землетрясений для Южной Камчатки (Викулин, 1992).
Поперечная миграция в направлении от береговой линии к желобу проходит со скоростью
VK-K^ = 0,3-0,4 км/год, (VK-K^)max = 1 км/год (2.3.6)
Близкое значение для поперечной скорости миграции камчатских землетрясений с М ³ 7, равное 1,5 км/год, было получено в работе (Вилькович, Шнирман, 1982).
В классе сильных камчатских, как и сильнейших северо-западно-тихоокеанских, землетрясений так же имеет место совпадение особых «пространственных» Мsg (1.2.1) и «временных» Ме01 (2.2.4) и Ме1 (2.2.6) значений магнитуд:
Msg = 5,3 » Мt01 = 5,1±0,3 = Mst .(23.7)
Поэтому сильные землетрясения так же закономерным образом должны быть распределены в пространстве-времени.
На приведенном выше рис. 1.4.4 по землетрясениям энергетических классов К³7 (М³1) выделена зона сейсмического затишья и по К³10-11 (М³3-4) сейсмическая дыра. При этом сильные землетрясения закономерным образом перемещаются (мигрируют) вдоль границы дыры против часовой стрелки со скоростью по порядку величины, равной значению n = 2оборота/(1997-1977)год » 0,1 год-1 и V = l×n » (1-10)км/год.
По сути, близкое явление циклической миграции, протекающее со скоростью около 11 км/год на материале землетрясений вблизи г. Душанбе, отмечено в работе (Сирожева, Кулагин, 1976).
Исследовались особенности графика повторяемости землетрясений. При анализе использовались две совокупности данных, описанных в разделе 2.2: землетрясения с М ³ 7, происшедшие в пределах северо-западной окраины Тихого океана в 1904–1981 гг. (N=264, табл. 2.3.1), и с К ³ 10 (М ³ 3), происшедших на Камчатке в 1962-1980 гг. (N=1886) в очагах сильнейших землетрясений 4.11.1952, М=8,5, 4.5.1959, М=7,6 и 15.12.1971, М=7,8 в течение различных стадий сейсмического цикла. Данные о камчатских таких землетрясениях с К ³ 12,3 (М > 5) представлены в таблице 2.3.2. Графики повторяемости, построенные по этим совокупностям данных, представлены на рис. 2.3.3.
Наибольшее, превышающее удвоенное среднеквадратичное отклонение от закона повторяемости, построенного по данным о северо–западно-тихоокеанских землетрясениях, имеет место в точке М = 7,6. Методом оценки индивидуального отклонения (Закс, 1976) величины lgN можно показать, что отклонение от закона повторяемости в этой точке значимо на уровне 0,05. Как видно из данных, представленных в табл. 2.3.1, в малой окрестности этой же точки имеют место локальные минимумы чисел землетрясений по данным для каждой островной дуги в отдельности.
Таким образом, распределение северо-западно-тихоокеанских землетрясений с М ³ 7 по их сейсмическим энергиям имеет особенность в окрестности точки
МЕ = 7,6 ± 0,1. (2.3.8)
Из данных, представленных в таблице 2.2.2 и на рис. 2.2.3, аналогичным образом сделан вывод о том, что энергетическое распределение камчатских землетрясений, происшедших в очагах сильнейших событий в течение любой стадии сейсмического цикла, имеет особенность в окрестности точки
Кe = 12,5 ± 0,1 , Мe = 5,3 ± 0,1. (2.3.9)
Cледует отметить, что статистически значимые отклонения от линейного закона повторяемости в областях магнитуд, соответствующих классам сильнейших и сильных землетрясений, ранее отмечались многими исследователями (см. Введение. С. 6).
В работе (Кузнецова, 1974) высказывается предположение о том, что причины искажения графика повторяемости как в области слабых, так и в области сильных землетрясений могут быть вызваны их взаимодействием.
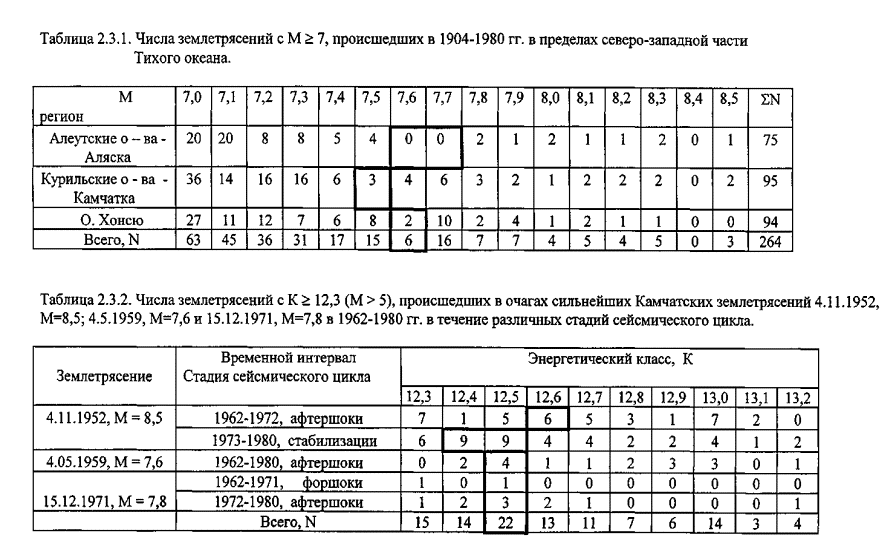
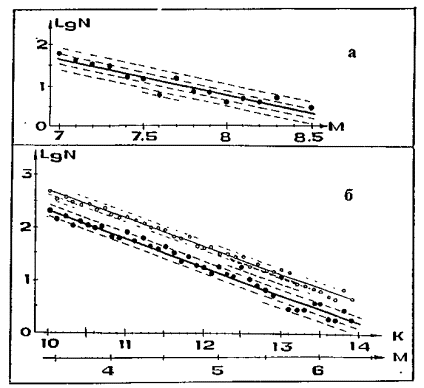
Рис. 2.3.3. Графики повторяемости северо–западно-тихоокеанских 1904–1980 гг., М ³ 7 (а) и камчатских 1962–1980 гг., К ³ 10 (М ³ 3) (б) землетрясений. Не залитые кружки и тонкая прямая линия соответствуют графику повторяемости, построенному по данным о всех камчатских землетрясениях 1962–1980 гг.
Итак, для каждого из классов сильнейших (S-T-E) и сильных (s-t-e) землетрясений, как видно из равенств (2.3.1) и (2.3.8), с одной стороны, и (2.3.7) и (2.3.9) – с другой, были получены следующие равенства:
МЕ = МST = 7,7±0,2 (2.3.10)
Me = Mst = 5,3±0,3 (2.3.11)
которые показывают, что пространственно-временным закономерностям распределения очагов землетрясений в каждом классе событий соответствуют особенности энергетического распределения. Физически этот вывод равносилен утверждению, согласно которому очаги землетрясений в пределах каждого класса событий (сильных или сильнейших) можно рассматривать как взаимодействующие. Следовательно, соответствующие миграционные цепочки можно считать проявлением такого взаимодействия.
Сформулированный нами вывод о существовании взаимодействия между землетрясениями является принципиально новым физическим результатом, который основан на равенстве значений, соответствующих особенностям пространственно-временных и энергетических распределений сейсмичности.
Ранее отмечалось наличие взаимосвязи между землетрясениями как всей планеты (Вилькович, Прозоров, Хадсон, 1976; Стовас, 1958), так и отдельно взятых ее регионов, таких как тихоокеанское кольцо (Кузнецов, Кейлис-Борок, 1997), Аляска (Bowman, Kisslinger, 1985), Япония (Okada, 1978), Камчатка (Кондратенко, 1971), Кавказ (Лурсманашвили, Качахидзе, 1980) и др. (Гайский, 1970). Такой вывод основывался на доказательстве математического утверждения о величине соответствующей статистической значимости эффекта. Очевидно, что оба эти вывода дополняют друг друга и могут рассматриваться как доказательство существования взаимодействия между очагами землетрясений на разных масштабных пространственно-временных и энергетических уровнях.
Полученные данные позволяют конкретизировать эффекты «притяжения» и «отталкивания» землетрясений, которые были установлены при исследовании свойств распределения землетрясений во времени (раздел 2.2). А именно, «отталкивание» землетрясений, очевидно, можно связать с таким свойством их очагов, как непересечение друг с другом «элементарных» блоков и сейсмических дыр для классов сильнейших и сильных землетрясений соответственно. Тогда класс форшоков и афтершоков, которые «втягиваются» внутрь очагов более сильных событий, может быть связан с эффектом «притяжения» землетрясений.
Рассмотрим класс сильнейших тихоокеанских землетрясений. Для этого класса событий сейсмофокальную зону можно считать одномерной и эффект миграции их очагов математически можно записать следующим образом:
aх ± bt = 0, V = b/a, (2.3.12)
где х – координата очага землетрясения вдоль зоны, t – время, a и b – коэффициенты, V – скорость миграции.
Изменение сейсмической активности как функции времени в пределах очага сильнейшего землетрясения, в соответствии с представлениями сейсмического цикла (см. раздел 1.2), имеет d-образный вид: в течение небольшого интервала (много меньше продолжительности сейсмического цикла или квазипериода) в момент сильнейшего толчка сейсмическая активность в его очаге увеличивается на много порядков. Тогда, в соответствии с соотношением (2.3.12), для величины сейсмической активности А(х, t) в пределах окраины Тихого океана, как функции пространственной координаты и времени, справедливо соотношение:
А(х, t) = Ф(ах ± bt), (2.3.13)
где Ф – произвольная функция.
Цикличность (Ф ~ exp(iwtt)) и квазипериодичность (Ф ~ exp(ixwsp/U)) сейсмического процесса накладывают следующие условия на функцию Ф:
Ф ~ exp[i(wtt ± xwsp/U)], а = iwsp/U, b = iwt, V = Uwt/wsp, (2.3.14)
где wt = 2p/Tt, wsp =2p/Tsp, U – скорость волны. Из соотношений (1.1.2) и (2.2.3) видно, что значения «пространственного» Тsp (сейсмический цикл) и «временного» Tt периодов сейсмического процесса близки друг другу: Тsp = 190 ± 40 » Tt = 230 ± 60 (лет), откуда из соотношения (2.3.14) получаем равенство скоростей V » U.
Таким образом, полученные данные показывают, что взаимодействие в классе сильнейших землетрясений, по сути, является волновым процессом, что проявляется в виде миграции их очагов в пространстве и во времени.
Данные, приведенные в разделе 1.3, показывают, что аналогичный вывод на меньшем масштабном уровне справедлив и для класса сильных землетрясений.
Закономерное распределение землетрясений в пространстве-времени позволяет предложить и физически и математически прозрачную методику прогноза времени толчков и мест расположения их очагов. По-видимому, впервые на возможность построения прогноза землетрясений, в основе которого заложены представления об их миграции, указал M.Bath (1966). Очень близко к разработке такой методики подошел К.Моги (Mogi, 1968, 1969). Вероятно, отсутствие в то время физических механизмов, объясняющих волновую природу миграции, не позволило К.Моги довести свои исследования до методических рекомендаций.
Попытка практического применения эффекта миграции землетрясений для целей прогноза времени сильных японских землетрясений и мест расположения их очагов была предпринята в работе (Kisslinger, 1974).
С использованием выявленных миграционных закономерностей нами были построены схемы долгосрочного прогноза времени землетрясений и мест расположения их очагов (Викулин, 1986, 1989, 1990, 1992, 1994, 1999). При расчете наших прогнозных схем использовались данные о глабальной и локальной миграции. Вместо данных о локальной миграции могут быть использованы и данные о повторяемости землетрясений в пределах отдельно взятых локальных регионов (сейсмофокальных блоков). В основе методики, как изначально и предполагалось (Bath, 1966), закладываются известные данные о положении и времени первого события в цепочке и о направлении и величине скорости миграции.
Опираясь на данные о миграционных цепочках (рис.2.3.1), для северо-западной окраины Тихого океана, включающей Японскую, Курило-Камчатскую и Алеутскую вместе с Аляской островные дуги был построен долгосрочный прогноз, который содержит указание мест расположения очагов сильнейших землетрясений и интервалов времени, в течение которых такие землетрясения можно ожидать (Викулин, 1989). Прогноз был построен в двух вариантах. Прогноз (I) был рассчитан для среднего временного интервала между миграционными цепочками, прогноз (II) - в предположении, что величина временного интервала между цепочками изменяется неким закономерным образом. «Предпоследние» сильнейшие землетрясения в регионе: Шикотанское 4.10.1994, М=8 и вблизи о. Хонсю 28.12.1994, М=7,9 - произошли в пределах пространственно-временных интервалов, предсказываемых прогнозом (I) и представленных на рис. 2.3.1, который, таким образом, следует считать более правильным.
В соответствии с таким прогнозом следующее сильнейшее землетрясение в пределах континентальной части п-ва Аляска (в месте, где 27.08.1904 произошло землетрясение с М = 8,3) можно было ожидать в период 1996–2004 гг. (Викулин, 1989). 4.11.2002 в этом месте Аляски произошло землетрясение с М = 7,9. Как видим, долгосрочный прогноз для северо-западной части Тихого океана, основанный на закономерностях миграции, достаточно хорошо оправдывается.
С использованием макросейсмических и инструментальных данных о 15 землетрясениях с М ³ 7,9, происшедших в 684-1946 гг. (рис. 2.3.2), был построен долгосрочный прогноз для сильнейших землетрясений с очагами вблизи желоба Нанкай, который включает тихоокеанское побережье о-вов Сикоку и Хонсю до г. Токио включительно (Викулин, Викулина, 1989; Викулин, 1987, 1992). При построении прогноза были учтены следующие данные: весь регион оказалось возможным разбить на три примерно равные по протяженности 270 ± 30 км зоны; очаги сильнейших землетрясений объединяются в цепочки, в пределах которых они мигрируют из одной зоны в другую в направлении с северо-востока на юго-запад; в пределах каждой зоны сильнейшие землетрясения имеют тенденцию повторяться через 128 ± 44 года и их очаги мигрировать в сторону береговой линии со скоростью 0,17 ± 0,04 км/год с характерным временем около 600 лет. Согласно этому прогнозу следующее сильнейшее (М ³ 7,9) землетрясение в пределах этого региона должно произойти в 2070 ± 40 году. При этом его макросейсмический эффект должен быть на 1,0 ± 0,5 балла MSK-64 больше, чем при последних сильнейших нанкайских землетрясениях 1923, 1944 и 1946 гг. Возможен вариант, при котором с небольшим интервалом в соседних зонах произойдут два землетрясения. Такие пары землетрясений происходили в 1605 и 1707 гг. - практически одновременно, в 1854 гг. - с интервалом в один день и в 1944 и 1946 гг. - с интервалом в два года.
Анализ пространственно-временных закономерностей распределения сильнейших землетрясений 1737-1971 гг., происшедших у берегов северных Курил-Камчатки (Викулин, 1986, 1984, 1987, 1990), позволил для этого региона построить долгосрочный прогноз (Викулин, 1992, 1994), представленный на рис. 2.3.2 и 2.3.4. Согласно этого прогноза ближайшие сильнейшие (М ³ 7,6) землетрясения должны произойти в пределах Кроноцкого в 1998-2019 гг. и южно-камчатского с вероятностью около 70% в 2008 ± 10 году и с 95% - в 2008 ± 20 году сейсмофокальных блоков. В южно-камчатском блоке очаг, скорее всего, должен располагаться в центральной части блока на равном удалении от береговой линии и от оси глубоководного желоба. Макросейсмический эффект таких землетрясений в г. Петропавловск-Камчатском не должен превышать 7±1 балла MSK-64. При построении прогноза использовались данные о блоковом строении сейсмофокальной зоны, о повторяемости сильнейших землетрясений в блоке через 108±7 лет, о двух типах «продольной» миграции (раздел 2.3) и о миграции очагов вкрест береговой линии со скоростью 0,3-0,4 км/год.
Использовать эффекты миграции и повторяемости землетрясений для цели прогноза их времени и места вслед за (Bath, 1966), по-видимому, впервые было предложено в работе (Kisslinger, 1974).
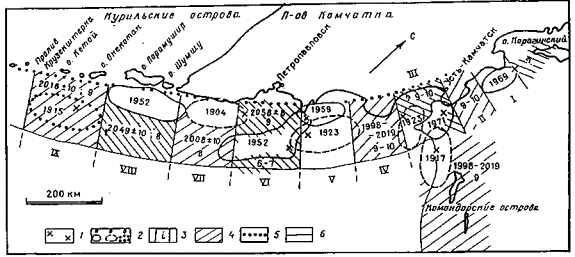
Рис. 2.3.4. Прогнозная карта расположения будущих очагов сильнейших камчатских и северо-курильских землетрясений. 1 - эпицентры сильнейших землетрясений; 2 - уверенные (а), менее уверенные (б) и вероятные (в) границы очаговых областей сильнейших землетрясений ХХ в.; цифра обозначает год сильнейшего землетрясения; 3 - границы между блоками сейсмофокальной зоны, i = I-IX; 4 - места вероятного расположения будущих очагов сильнейших землетрясений; цифрами обозначены: год ожидаемого землетрясения, временной интервал и максимальное значение сотрясений на берегу (в баллах MSK – 64) при землетрясении; 5 - западная граница сейсмофокальной зоны; 6 - ось глубоководного желоба.
7-8.03.1999 г. в Авачинском заливе (рис. 1.4.4) произошла серия землетрясений, наиболее сильные (4,8 £ М £ 6,7) из которых ощущались в Петропавловске-Камчатском с интенсивностью до 3-5 баллов. Очаги этих землетрясений, по сути, продолжили «вихревую» со скоростью 1-10 км/год цепочку событий, наблюдающуюся с 1962 г. На этом основании автором был дан прогноз, согласно которому землетрясения 7-8.03.1999 г. не являются форшоками более сильного землетрясения с очагом в Авачинском заливе (Викулин, 1999). Сделанный прогноз оправдался.
5.12.1997 в пределах Кроноцкой сейсмической бреши (рис. 2.3.4) произошло землетрясение, магнитуда которого по данным некоторых сейсмических станций достигала М=8. Если считать, что это землетрясение относится к классу сильнейших, как имеющее магнитуду М ³ Мsp = 7,6 (см. раздел 1.1), то можно принять прогноз, построенный в (Викулин, 1992, 1996) и представленный на рис. 2.3.4, оправдавшимся, так как согласно этому прогнозу сильнейшее землетрясение с очагом в кроноцком сейсмофокальном блоке должно произойти в 1998-2019 гг.
С.А.Федотов с соавторами (Федотов и др., 1998) полагают, что 5.12.1997 г. в пределах Кроноцкой бреши действительно произошло сильнейшее землетрясение. В соотвествии с таким прогнозом в данном месте в течение сейсмического цикла, т.е. в течение последующих 100-200 лет, сильнейшее землетрясение не должно произойти. Согласно же нашим данным (Викулин, 1998) пока не достаточно оснований считать долгосрочный сейсмический прогноз для кроноцкой сейсмической бреши реализованным. По следующим причинам.
1. Магнитуда Кроноцкого землетрясения Мкр, определенная по всем имеющимся данным, меньше порогового значения Мsp = 7,6 (раздел 1.1), определяющего принадлежность камчатских землетрясений к классу сильнейших событий: Мкр = 7,55 < Мsp. В том числе, значения и макросейсмической и цунами магнитуд, величины которых для Кроноцкого землетрясения составили 7,2-7,3, являются очень низкими для класса сильнейших землетрясений.
2. Многочисленные сильные афтершоки Кроноцкого землетрясения в течение первого месяца чаще происходили на краю бреши при минимуме активности в ее центральной части, что, как показано в разделе 1.2, является не характерным для очагов сильнейших землетрясений в течение первой фазы афтершоковой стадии. Такое распределение сильных толчков в соответствии с правилом «краевой сейсмичности» (раздел 1.2) характерно для других стадий сейсмического цикла.
3. Сильные землетрясения, магнитуды которых несколько меньше пороговых значений, часто происходят в очагах сильнейших землетрясений на форшоковой и афтершоковой стадиях. Например, в пределах очага Итурупского 6.11.1958, М=8,2 землетрясения 21.02.1937 г. произошел толчок с М = 7,6 (для Южных Курил пороговое значение магнитуды составляет Мsp = 7,9), который сопровождался большим количеством афтершоков с М ³ 6 (Новый каталог, 1977). В пределах южной оконечности очага Большого Камчатского землетрясения 4.11.1952, М=8,5 через 21 год после него 28.02.1973 г. произошло Парамуширское землетрясение с М=7,5, которое сопровождалось большим количеством сильных афтершоков.
Инструментальные данные о сильнейшем землетрясении с очагом в пределах Кроноцкой сейсмической бреши не известны. Реконструкция сейсмического процесса Камчатки и Северных Курил, проведенная с использованием представлений о миграции и повторяемости землетрясений (Викулин, 1992), позволяет предположить, что таким событием могло бы быть землетрясение с М=7,9, происшедшее 23.11.1899. В таком случае можно принять следующую гипотезу: Кроноцкое землетрясение 5.12.1997 г., являясь форшоком, указывает на возможность того, что в пределах Кроноцкой сейсмической бреши в течение ближайших десятилетий может произойти сильнейшее землетрясение с М ³ Мsp = 7,6.
Анализ особенностей распределения землетрясений в пространстве и во времени позволил установить, что сильные землетрясения Австралии мигрируют вокруг материка со скоростью около 50 км/год. Полученные данные позволили построить прогноз (рис. 1.4.3), согласно которому наиболее активным в ближайшие десятилетия должно являться северо-западное побережье Австралии (Викулин, 1994).
Сводки данных о наиболее сильных форшоках и афтершоках с М ³ 6 в очагах сильнейших землетрясений северо-западной окраины Тихого океана, происшедших в 1904-1978 гг., представлены в табл. 2.2.1-2.2.3 (и, см. далее, 3.1.1). Как видно из данных, представленных в этих таблицах, наиболее сильные форшоки и афтершоки имеют примерно одинаковые магнитуды, равные 7,3-7,4. Форшоки с такой магнитудой происходят в очагах примерно 10% японских, 40-50% камчатских и 70-90% курильских сильнейших землетрясений, в среднем, в 40-50% сильнейших северо-запандно-тихоокеанских землетрясений. Такой «форшоковый» процент отмечен и по мировым данным (Parazachos at.ol., 1967; Prochazkova, 1973; Suzuki, 1982). Перед сильнейшими толчками форшоки с М ³ 7 происходят, в среднем, в течение 11 часов; 80% из них происходят в течение одного месяца. Афтершоки с М ³ 7 - происходят, в среднем, через 3 дня после главных толчков, практически все из них - в течение 3 месяцев.
Предпосылками для включения инерционных эффектов, связанных с вращением Земли, в перечень основных параметров, определяющих сейсмический (сейсмотектонический) процесс, являются следующие данные.
Во-первых, при тектоническом движении плиты друг относительно друга смещаются как упругие целые образования. Пластическая деформация оказывается достаточно большой лишь в пределах достаточно узких зон и ее локализация не однородна. В таком случае, слагающие ее объемы, как показывают экспериментальные данные (Панин, Гиряев, Лихачев, 1987; Владимиров, Романов, 1986), могут поворачиваться. Инерционные силы, приводящие к такому вращению, относятся к объемным силам и напряжения, созданные внутри него, нельзя срелаксировать за счет пластической деформации.
Во-вторых. Сейсмофокальная зона, в пределах которой осуществляется межплитовое пластическое течение, представляет собою тонкий слой. Линейные размеры слагающих его блоков составляют первые сотни километров. При таких размерах (очагов сильнейших землетрясений) инерционные эффекты, вызванные вращением Земли, являются значительными и приводят к повороту блоков (Daly, 1989; Геологическая..., 1989; Geist, Childs, Scholl, 1988; Nur, Scotti, 1986). На возможность существования такого рода поворотных движений указывают данные геодезических наблюдений, проведенных в Японии в течение 80 лет (1909-1987 гг.). Согласно этим данным, о.Хоккайдо и другие районы японских островов, захваченные вихревыми структурами, центры которых располагаются вблизи залива Сагами (центральная часть о. Хонсю) и о. Сикоку, включая рядом расположенные о. Кюсю и юго-западную часть о. Хонсю, вращаются по часовой стрелке (Рикитаке, 1970; Мелекесцев, 1979; Hashimoto, Tada, 1988).
В-третьих. Продолжительность сейсмического цикла, как показано в разделе 1.2, достаточно велика и составляет 100-200 лет. Такой продолжительный отрезок времени может привести к тому, что накапливаемые обычным способом в очаге готовящегося землетрясения напряжения будут в значительной степени срелаксированы. Инерционные же напряжения срелаксировать за счет пластической деформации невозможно, поскольку для этого, как отмечалось выше, требуется блок (и всю планету) повернуть в начальное состояние.
В-четвертых, исследование дислокационных моделей механизмов очагов некоторых сильнейших землетрясений показало их плохое соответствие общепринятой модели плоской бесконечной дислокации в однородном пространстве (Shamsi, Stacy, 1969; Mount, 1987; Guo, 1988). В то же время, блочное (плитовое) строение литосферы проявляется в виде относительных поворотов.
Таким образом, в пределах сейсмофокальной зоны тихоокеанского кольца существуют условия, при которых может быть реализован ротационный механизм. А именно, вследствие вращения планеты напряжения возникают вокруг поворачивающегося блока сейсмофокальной зоны.
Предпосылками для включения инерционных эффектов, связанных с вращением Земли, в перечень основных параметров, определяющих сейсмический (сейсмотектонический) процесс, являются следующие данные.
С одной стороны, из тектоники и физики твердого тела известно следующее. Во-первых, при тектоническом движении плиты друг относительно друга смещаются как упругие целые образования, внутри которых отсутствуют пластические деформации. Аккомодационный слой, в пределах которого пластическая деформация оказывается достаточно большой, заключен лишь в пределах узких зон. При таком механизме соприкосновения плит упругие напряжения, появляющиеся из-за противодействия движению, быстро снижаются с удалением от их краев. Скорость пластического течения для твердых тел, как известно (Хирт, Лоте, 1972), пропорциональна экспоненте от сдвигового напряжения. Именно такое соотношение между скоростью пластического течения и величиной сдвигового напряжения и является одной из главных причин сильной локализации пластической деформации. При этом, небольшое увеличение напряжения приводит к росту скорости пластического течение в 10-100 и более раз.
Во-вторых, зона локализации пластической деформации, оказывается, может не быть однородной. Экспериментальные данные показывают, что при пластической деформации образца некоторые его объемы могут двигаться как целые и, в частности, вращаться. Например, экспериментально установлено (Панин, Гиряев, Лихачев, 1984; Владимиров, Романов, 1986), что при растяжении поликристаллических образцов в области интенсивных пластических деформаций некоторые зерна поворачиваются на десятки и более градусов как целые без пластической деформации внутри. При этом установлено, что «ротации для кристаллической решетки являются столь же типичными, как и турбулентное течение для жидкости» (Панин, Гиряев, Лихачев, 1984). Вокруг таких зерен существует тонкий аккомодационный слой, в котором происходит пластическая деформация. При этом сплошность образца не нарушается, и средняя величина пластической деформации составляет несколько процентов. В определенных случаях такой поворот некоторых объемов как целых с достаточно узкой зоной высокой пластической деформации по краям становится энергетически более выгодным, чем равномерное деформирование всего образца. Природа сил, вызывающих поворот зерен в поликристаллических образцах, до конца пока не установлена.
Следует отметить, что в силу малости размеров зерен, инерционные эффекты, связанные с вращением Земли, чрезвычайно малы и по этой причине в экспериментах такие эффекты не отмечены.
В-третьих. Инерционные силы, приводящие к повороту (вращению) относятся к объемным силам, в отличие от упругих сил, которые, по сути, действуя на контактах, являются поверхностными. Это означает, что при вращении образца напряжения, созданные внутри него в результате поворота его некоторых частей, нельзя срелаксировать за счет пластической деформации. Для релаксации таких напряжений весь образец необходимо соответствующим образом поворачивать как целое.
С другой стороны, данные о пространственно-временных параметрах сейсмического процесса, геологические данные о блоковом строении сейсмофокальной зоны и данные о физических условиях, в которых находится вещество в очагах землетрясений, показывают следующее.
Во-первых. Сейсмофокальная зона, в пределах которой осуществляется межплитовое пластическое течение на глубинах Н > 70 км, представляет собою тонкий слой, падающий под материк под некоторым углом. В верхней своей части (H < 70-100 км), в пределах которой происходит большая часть землетрясений и в том числе практически все сильнейшие, сейсмофокальная зона имеет блоковое строение. Линейные размеры блоков в плане составляют 50-200 км «в ширину» (вкрест простирания сейсмофокальной зоны) и 100-1000 км «в длину» (протяженность очагов сильнейших землетрясений). «Толщина» разломов, рассекающих сейсмофокальную зону, не превышает, по-видимому, первые километры.
При таких параметрах блоков (очагов сильнейших землетрясений) инерционные эффекты, вызванные вращением Земли, могут быть весьма значительными.
Во-вторых, геологическое строение островных дуг и континентальных окраин Тихого океана указывает на то, что блоки, слагающие верхнюю часть сейсмофокальной зоны, вращаются. Так в работе (Daly, 1989) показано, что такие блоки в районе тихоокеанского побережья Эквадора вращаются по часовой стрелке. Вращение сейсмофокальных блоков центральной части Алеусткой дуги также по часовой стрелке, как полагается в работе (Геологическая..., 1989), по-видимому, началось в конце миоцена-плиоцене и обусловлено наличием сдвиговой компоненты при косом поддвиге тихоокеанской плиты под северо-американскую плиту. При этом, значение угла поворота для разных блоков лежат в пределах 0-23о(Geist, Childs, Scholl, 1988). Механизм вращения геологических блоков вблизи разлома Сан Андреас обсуждался в (Nur, Ron, Scotti, 1986).
Видим, что строение верхней части сейсмофокальной зоны допускает выполнение необходимых условий, при которых повороты слагающих ее блоков становится вполне возможным.
В-третьих. Период повторяемости сильнейших тихоокеанских землетрясений в пределах одного блока сейсмофокальной зоны достаточно продолжительный (порядка 100 лет). Температура вещества, слагающего очаг землетрясения, велика: на глубинах в десятки километров (50-100 км) она достигает сотен градусов (1000-15000С). Эти данные указывают на то, что накопление напряжений в очаге землетрясения «обычным» способом может быть сильно затруднено. Действительно, при высокой температуре внутри очага землетрясения величина пластической деформации, вследствие ее экспоненциальной зависимости от температуры, может приближаться к упругой и составить доли процента. При большом времени подготовки землетрясения это обстоятельство может привести к полной (или, во всяком случае, к значительной) релаксации напряжений, накапливаемых в очаге готовящегося землетрясения обычным способом. Инерционные же напряжения, которые могут возникнуть вследствие вращения Земли, как отмечалось выше, срелаксировать за счет пластической деформации невозможно
В-четвертых, исследование дислокационных моделей механизмов очагов некоторых сильнейших землетрясений показало их плохое соответствие модели плоской бесконечной дислокации. Так, например, механизмы очагов Калифорнийского 1906, М=8 и Аляскинского 1964, М=8,3 землетрясений наилучшим образом согласуются с сейсмологическими и геодезическими данными в рамках модели винтовой дислокации (Shamsi, Stacy, 1969).
Таким образом, проведенный анализ показывает следующее. В пределах сейсмофокальной зоны тихоокеанского кольца существуют условия, при которых может быть реализован ротационный механизм. А именно, вследствие вращения планеты напряжения возникают вокруг поворачивающегося блока сейсмофокальной зоны. И такой механизм может оказаться более реальным по сравнению с общепринятым в настоящее время механизмом накопления напряжений, в основе которого заложены процессы, приводящие к появлению внутри очага так называемого магистрального разрыва.
Приведенные выше данные позволяют разработать ротационную модель, в основе которой заложены инерционные эффекты, связанные с вращением тела, и применить ее для описания закономерностей сейсмического процесса. Ниже покажем, что для этого имеются все основания. Для этого в качестве вращающегося тела рассмотрим Землю, в качестве элементарных поворачивающихся объемов - блоки земной коры, слагающие сейсмические пояса. Такие блоки вдоль окраины Тихого океана будем называть сейсмофокальными.
Рассчитаем поле упругих напряжений, возникающих вокруг поворачивающегося за счет своих внутренних источников макрообъема V, являющегося частью твердого тела, вращающегося с угловой скоростью W .
При рассмотрении природы возникновения поля упругих напряжений в твердом теле вокруг поворачивающегося объема (блока) V необходимо учесть два обстоятельства, имеющих принципиальное значение.
Во-первых. Инерционные силы, вызванные вращением тела, всегда связаны с элементом конечного объема. Такие силы, в принципе, нельзя определить для произвольно малого объема, как это, например, делается для силы тяжести и других подобных сил. Это связано с тем, что вращательные инерционные эффекты зависят не только от массы блока, но и от ее распределения по его объему, т.е. от момента инерции I, который для точки всегда равен нулю. Момент импульса М блока V запишется в виде М = I* W, где W- угловая скорость вращения объема V, равная скорости вращения тела и направленная параллельно оси его вращения.
Во-вторых. Поворот блока V происходит во вращающемся теле; связанная с ним система координат является неинерциальной. Как известно, в таких системах появляются дополнительные силы, как, например, центробежная и сила Кариолиса. Математическое описание процессов, происходящих в неинерциальных системах, в значительной степени зависит от выбора системы координат.
При этих условиях, механизм появления упругих напряжений, возникающих во вращающемся твердом теле при повороте некого объема V внутри него, можно определить следующим образом.
До поворота блок V имел момент импульса М, который был направлен вдоль оси Z, параллельной оси вращения тела. В результате поворота блок V поворачивается в некой плоскости на угол b относительно оси вращения тела. Если бы блок V не был бы связан с окружающей его средой, то при его повороте момент импульса М изменил бы свое направление и никаких изменений в окружающем блок пространстве не произошло бы. Однако, в случае когда объем V упруго «сцеплен» с окружающей его средой, изменение направления момента импульса блока приводит к появлению вокруг него упругих напряжений, которые в силу законов механики должны характеризоваться соответствующим моментом силы.
Решение задачи проведем в три этапа.
1. Рассмотрим две системы
координат, которые повернуты друг
относительно друга вокруг общей оси Y на
угол b. Ось Z первой (исходной) системы
координат параллельна оси вращения тела и
направлена от южного полюса к северному,
ось ![]() второй системы параллельна моменту
импульса блока V после его поворота на угол b. Начала обоих систем координат
находятся в центре масс области V (рис. 2.4.1).
второй системы параллельна моменту
импульса блока V после его поворота на угол b. Начала обоих систем координат
находятся в центре масс области V (рис. 2.4.1).
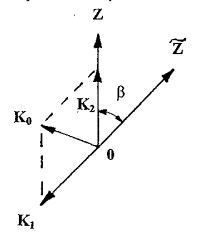
Рис. 2.4.1. Две системы координат, повернутых относительно общей оси на угол b. Ось Z параллельна оси вращения тела и направлена от его южного полюса к северному.
Для определения величины упругих напряжений, возникающих вокруг поворачивающегося блока V, применим следующий мысленный эксперимент.
Сначала останавливаем вращение
объема V, прикладывая упругие напряжения s1 с моментом силы К1, направленным в
отрицательном направлении оси ![]() . При этом считаем, что кинетическая энергия
вращения области V полностью переходит в
потенциальную энергию упругих напряженийs1 . Затем, прикладывая
упругие напряжения s2 с моментом силы К2, направленным вдоль оси Z,
блок V опять раскручиваем до скорости
вращения тела (рис. 2.4.1).
. При этом считаем, что кинетическая энергия
вращения области V полностью переходит в
потенциальную энергию упругих напряженийs1 . Затем, прикладывая
упругие напряжения s2 с моментом силы К2, направленным вдоль оси Z,
блок V опять раскручиваем до скорости
вращения тела (рис. 2.4.1).
Другими словами, когда тормозим область V, ее кинетическая энергия вращения
W = 1/2IW 2 (2.4.1)
переходит в упругую энергию, определяемую тензором напряжений s1 , а когда раскручиваем - мы создаем точно такую же кинетическую энергию, но за счет упругих напряжений s2 .
Рассмотрим случай, когда объем V представляет собой однородный шар, момент инерции которого, как известно, не зависит от выбора оси вращения. Тогда равенство кинетической и потенциальной энергий приводит к соотношению | К1|=|К2| . При этом разность этих векторов и является искомым моментом силы К0, возникающим в результате поворота блока V в неинерциальной системе: К0 = К2 - К1. Его модуль получаем из теоремы косинусов:
| К0| = 2| К1| sinb /2 (2.4.2)
2. Искомое поле упругих деформаций U, как известно (Ландау, Лифшиц, 1965), должно удовлетворять уравнению упругого равновесия:
graddivU -a*rotrotU = 0 (2.4.3)
с нулевыми граничными условиями на бесконечности:
U ®0 при r ® ¥ (2.4.4)
с действующей на объем V силой, равной нулю:
Fi = ![]() = 0
(2.4.5)
= 0
(2.4.5)
и моментом силы, не зависимым от размера блока V:
Кi =![]() , (2.4.6)
, (2.4.6)
где а=(1-2n ) / 2(1-n ),n - коэффициент Пуассона, R0 - радиус области V.
Решением задачи (2.4.3) - (2.4.6) в сферической системе координат (r, j, u ) с началом r = 0 в центре шарового объема V в области r ³R0, являются поля смещений U и напряжений s.
Ur = U0 = 0, Uj = -3Аr-2sinu (2.4.7)
srj = sjr = 3/2АGr-3sinu (2.4.8)
где G - модуль сдвига, А - константа, которая будет определена ниже. Остальные компоненты тензора напряжений равны нулю.
Подставляя (2.4.8) в (2.4.6) для момента силы, который создает найденное упругое поле, получаем выражение:
K1z = 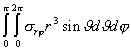 = 3p2AG
(2.4.9)
= 3p2AG
(2.4.9)
Остальные компоненты момента силы, вследствие выбора системы координат, равны нулю K1x = K1y = 0 (рис. 2.4.1).
3. Плотность энергии упругих
деформаций записывается следующим образом:
W = ![]() , где
l- модуль всестороннего сжатия, e
ij - деформация и d
ij - символ Кронекера.
Интегрируя это выражение по всему объему
тела и считая его несжимаемым, получим
следующее выражение для величины упругой
энергии, созданной моментом силы К1:
, где
l- модуль всестороннего сжатия, e
ij - деформация и d
ij - символ Кронекера.
Интегрируя это выражение по всему объему
тела и считая его несжимаемым, получим
следующее выражение для величины упругой
энергии, созданной моментом силы К1:
W = 9/2A2G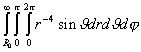 = 4pA2GR0-3
(2.4.10)
= 4pA2GR0-3
(2.4.10)
Приравнивая полученную упругую энергию кинетической (2.4.1) и учитывая, что момент инерции шара равен I=8/15pr R05, где r - плотность вещества, получаем следующее выражение для величины искомой константы А:
A = ![]() (2.4.11)
(2.4.11)
Таким образом, с учетом (2.4.2) для искомых решений окончательно получаем следующие соотношения. Для момента силы упругого поля вокруг блока, направленного перпендикулярно плоскости его поворота:
K = -6p2WR04![]() sinb/2 (2.4.12)
sinb/2 (2.4.12)
величины упругой энергии:
W = 16/15prW 2R05sin2 b/2 (2.4.13)
поля смещений:
Ur = Uq = 0, Uj =-3WR04r-2 ![]() (2.4.14)
(2.4.14)
и напряжений:
srj = sjr = 3/2WR04r-3 ![]() . (2.4.15)
. (2.4.15)
Остальные компоненты напряжений равны нулю.
Появление в соотношениях (2.4.12) - (2.4.15) сомножителя sinb/2 , в соответствии с теоремой косинусов, по сути, является тривиальным «геометрическим» следствием задачи, решаемой в неинерциальной системе координат.
Как видим, полученные решения задачи о поле упругих напряжений вокруг поворачивающегося объема V действительно определяются величиной угловой скорости, с которой вращается тело, что и объясняет название модели, данное ей авторами - ротационная.
Следует отметить, что при форме блока, близкой эллипсоидальной или овальной, конечные формулы существенным образом не изменяются; в них, как показывают оценки, появляются коэффициенты порядка единицы.
Примем параметры модели: плотность среды r, модуль сдвига G, угловая скорость вращения Земли W, радиус «элементарного» шарового сейсмофокального блока, по объему равновеликого среднему очагу в классе сильнейших курило-камчатских и японских землетрясений, имеющих овальную (эллиптическую) форму R0 = (3/4´L/2´D/2´H)1/3 равными:
r = 3 г/см3; G = 1011 н/м2; W = 7,3×10-5 рад/с; R0 » 40-100 км. (2.4.16)
Здесь L = 150-200 км - протяженность вдоль сейсмофокальной зоны (длина), D = 75-100 км - «ширина» (размер вкрест зоны) и H = 50-100 км - «толщина» очага сильнейшего землетрясения - элементарного сейсмофокального блока. При таких значениях модельных величин любые три параметра из четырех: смещение U0, сброшенное напряжение s0, выделенная упругая (сейсмическая) энергия W0 и соответствующий ей момент силы (сейсмический момент) К0, как легко можно убедиться, автоматически из соотношений (2.4.12) - (2.4.15) получаются равными:
U0 ~ 10 м; s0 ~ 100 бар; W0 ~ 1016¸18 дж; К0 ~ 1028¸30 дин×см (2.4.17)
Эти значения достигаются при угле поворота блока:
b0 » U0 /R0 = 10-4 рад (» 10-2 град) (2.4.18)
Такое значение угла при повторяемости сильнейших землетрясений одно в 100 лет соответствует скорости поворота блока, равной 10-4град/год.
Следует отметить, что по порядку величины с примерно такой же скоростью поворачивается Исландия, протяженность которой, как и «элементарного» сейсмофокального блока, составляет около 200 км. Действительно, в соответствии с ротационной гипотезой, Исландия, вследствие вращения Земли, поворачивается по часовой стрелке; в результате чего в течение нескольких десятков тысяч лет линии трещинных извержений в ее южной части изменили свою ориентацию примерно на 70 с ССВ 25-270 в верхнем плейстоцене на ССВ 18-200 в послеледниковую эпоху (Мелекесцев, 1979).
Таким образом, проведенные оценки показали, что применение ротационной модели к расчету параметров очага сильнейшего землетрясения физически обосновано. Более того, сама возможность аналитического («комплексного» и «самосогласованного») описания нескольких физических величин в рамках одной модели без использования дополнительных данных (в том числе и данных инструментальных сейсмологических наблюдений о параметрах очагов землетрясений) указывает на ее определенные преимущества перед другими моделями очага тектонического землетрясения.
Концентрация упругой энергии в пределах окружающей блок части пространства и ее моментная природа позволяют предположить, что в рамках ротационной модели эффект взаимодействия очагов землетрясений может быть значительным.
Для определения величины энергии взаимодействия поворачивающихся блоков воспользуемся известной закономерностью, согласно которой упругая энергия (в рамках закона Гука) пропорциональна квадрату деформации. Тогда, записывая величину деформации какой-либо части твердого тела в виде суммы деформаций, создаваемых в этой части каждым из блоков в отдельности, получим выражение, в котором «перекрестное» слагаемое и определяет величину энергии взаимодействия блоков друг с другом.
Для модели двух блоков полную упругую энергию можно записать в виде:
W = G![]()
где a и b - тензоры упругой деформации, созданные в результате поворота первой и второй областями соответственно, интегрирование проводится по всему объему тела.
Первые два слагаемые в правой части в выражении для упругой энергии суть собственные упругие энергии, каждая из которых вычисляется с помощью соотношения (2.4.13). Третье слагаемое и определяет выражение для энергии взаимодействия первой и второй областей:
Wint = 2G ![]() (2.4.19)
(2.4.19)
Определим энергию взаимодействия. Положение двух блоков представлено на рис. 2.4.2. Система координат на этом рисунке выбрана следующим образом. Центры масс областей лежат на оси Х, расстояние между ними равно 2×l. Начало координат находится в середине отрезка, соединяющего центры масс. Ось Z выбрана таким образом, что вектор Kа
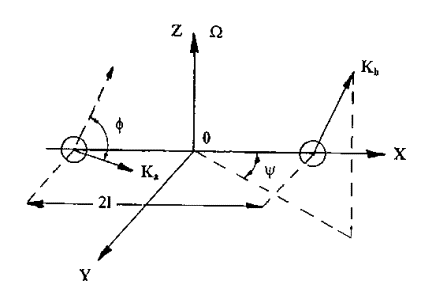
Рис. 2.4.2. Взаимная ориентация моментов сил Кa и Кb в модели двух блоков в прямоугольной системе координат XYZ. Ось Z параллельна оси вращения Земли W и направлена от ее южного полюса к северному, W - угловая скорость вращения Земли. f и y - углы, определяющие положение блоков, 2l - расстояние между их центрами тяжести.
лежит в плоскости XY и ось Y перпендикулярна этой плоскости. Направление оси Z выбрано так, чтобы система координат была правой.
Из рис. 2.4.2 видно, что ориентация вектора момента силы второй области Kb относительно такого же вектора первой области Ka может быть определена двумя углами: углом f между векторами Kb и Ka, который можно найти из соотношения cosf = (Ka´Kb)/|Ka|×|Kb|, и углом y между проекцией вектора Kb на плоскость XY и осью X. Матрица поворота вектора Kb в направлении вектора Ka записывается следующим образом:
½½ cosy×cosf -siny cosy×sinf ½½
Q = ½½ siny×cosf cosy siny×sinf ½½
½½ -sinf 0 cosf ½½
Тогда тензор b
в системе координат, задаваемой вектором Kb,
запишется в виде ![]() = QbQ/, где Q/ - транспонированная матрица.
= QbQ/, где Q/ - транспонированная матрица.
Полагая блоки шаровыми с радиусами R0a и R0b, записывая выражение для тензоров а и b через соответствующие им смещения (2.4.7), подставляя их в (2.4.1) с учетом (2.4.11) и производя вычисления соответствующих интегралов для энергии взаимодействия двух поворачивающихся областей получим следующее выражение:
Wint = 3/2prW2R0a4R0b4l-3cosf (2.4.20)
Энергия взаимодействия локализована в части пространства, расположенного вне блоков, где, как можно видеть из соотношения (2.4.19), оба тензора деформации не равны нулю:
Wint ¹ 0 при a ¹ 0 и b ¹ 0, т.е. при r ³ R0a, и r ³ R0b (2.4.21)
Вычисление интегралов проводилось в биполярной системе координат. При этом было сделано допущение, что расстояние l между областями много больше размера любой из областей. В этом случае при вычислении энергии взаимодействия оказалось возможным пренебречь размером соседней области и интегрирование проводить таким образом, как будто эти области точечные. Однако сделанное допущение не является принципиальным, поскольку всегда справедливо неравенство l ³ 2R0, a оценки показывают, что учет конечного размера областей дает поправку к результату второго порядка малости (R0a,b/l)2.
Момент силы, обусловленный энергией взаимодействия, можно определить путем дифференцирования соотношение (2.4.20) по углу f:
Kint = -3/2prW2R0a4R0b4l-3sinf (2.4.22)
Момент силы (2.4.22) приложен со стороны упругого поля к поверхности каждого из блоков и направлен таким образом, чтобы уменьшить величину энергии взаимодействия. Этот момент для обеих областей имеет одно и то же абсолютное значение, но для разных блоков он направлен в противоположных направлениях.
Таким образом, полные энергия W + Wint и суммарный момент силы K + Kint для каждого из блоков могут быть определены из соотношений (2.4.13), (2.4.20) и (2.4.12), (2.4.22) соответственно.
Будем полагать размеры обоих взаимодействующих объемов одинаковыми: R0a = R0b = R0. Тогда из соотношений (2.4.12) и (2.4.22) получаем примерно равенство:
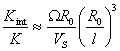 (2.4.23)
(2.4.23)
из которого видно, что инерционные эффекты взаимодействия, связанные с поворотом элементарных объемов внутри вращающихся тел, становятся тем более существенными, чем с большей скоростью W вращается тело и чем больше размер «элементарного» объема блока R0. VS = (G/r)1/2 - скорость поперечных волн.
Отношение энергии взаимодействия Wint к «собственной» энергии блока W на основании соттношений (2.4.13) и (2.4.20) определиться равенством:
![]() (2.4.24)
(2.4.24)
Из полученного равенства видно, что максимальное (cosf » 1) расстояние, на котором энергия взаимодействия будет по порядку величины близка собственной энергии блока (d » 1), определится из соотношения:
l0 ~ 2b-2/3R0 » (102¸103)R0 (2.4.25)
из которого видно, что упругие поля, создаваемые вокруг поворачивающихся объемов вращающегося тела, являются дальнодействующими. При получении численной оценки в (2.4.25) было использовано значение угла поворота блока из (2.4.18).
Дальнодействие, если оно реализуется в природе, должно приводить к тому, что сильнейшие землетрясения, происходящие в блоках с параллельно (f=0) [антипараллельно (f=p)] ориентированными моментами, должны происходить одновременно [не должны происходить вовсе]. Действительно, если в одном из таких блоков накопилась достаточная для сильнейшего землетрясения энергия, то в результате «параллельного» (f=0) взаимодействия как минимум такой же по величине энергией должен обладать и взаимодействующий с ним второй сейсмофокальный блок. В случае же «антипараллельного» (f=p) расположения моментов блоков энергия их взаимодействия, наоборот, компенсирует энергию, накапливаемую в готовящемся очаге. Имеющиеся сейсмологические данные, как нам представляется, подтверждают такой вывод модели.
В сейсмологической практике известны случаи, когда в течение небольшого интервала времени практически одновременно происходят два достаточно сильных землетрясения с близко расположенными очагами - так называемые дуплеты. Сильнейшие землетрясения-дуплеты происходят достаточно редко. В пределах северо-западной окраины Тихого океана нам известны следующие такие события, отмеченные независимо друг от друга разными исследователями на основании анализа макросейсмических данных, данных о цунами и инструментальных сейсмологических наблюдений: 31.1.1605, М=7,9 в районе желоба Нанкай (Соловьев, Го, 1974), 4.11.1952, М=8,5 в районе Северных Курил-Южной Камчатки (Попов, 1961; Викулин, Чернобай, 1986 а) и 13.10.1963, М=8,0 на Южных Курилах (Викулин, Чернобай, 1986 б). Реконструкция сейсмического процесса позволила сделать вывод о том, что землетрясения-дуплеты, близкие тем, которые отмечены в 1605 и 1952 гг., происходили 28.10.1707, М=8,4 в пределах желоба Нанкай (Викулин, Викулина, 1989) и 17.10.1737, М=8,4 на северных Курилах-южной Камчатке (Викулин, 1992). Кроме того, в работе (Викулин, 1992) было отмечено, что сильнейшие землетрясения-дуплеты на Камчатке, возможно, происходили и в 1790 и 1792 гг. Данные о расположении очагов сильнейших камчатских и нанкайских землетрясений по результатам работ (Викулин, 1990, 1996; Викулин, Викулина, 1989; Викулин, Гусяков, Титов, 1992) представлены на рис. 1.1.3, 2.3.2, 2.3.4.
Приведенные данные показывают, что сильнейшие землетрясения-дуплеты редко, но все же происходят. Можно выделить два района - желоб Нанкай и северные Курилы - южная Камчатка, в каждом из которых такие события отмечены, по-видимому, как минимум дважды. При этом, как было показано в работах (Викулин, 1990, 1992; Викулин, Викулина, 1989), с точки зрения пространственно-временных закономерностей (миграция, непересечение очагов и повторяемость в одном месте) эти толчки-дуплеты являются вполне «обычными» событиями.
Из данных, представленных на рис. 1.1.3, 2.3.2 и 2.3.4 также видно, что расстояние между очагами в дуплете примерно равно протяженности очага одного отдельно взятого толчка и составляет DL = 100-200 км. По данным японских источников (Соловьев, Го. 1974) два толчка 31.1.1605 г. произошли «практически одновременно». Анализ инструментального сейсмограммного материала показал, что при каждом их событий в 1952 и 1963 гг. толчки происходили с интервалом Dt = 4-5 сек (Викулин, Чернобай, 1986 а, б). При этом было отмечено, что второй толчок в каждом дуплете никак не мог быть следствием «перераспределения напряжений после первого толчка», так как скорость передачи «упругой» информации при этом должна была бы существенно превысить значение скорости продольных волн: DL/Dt » (20-50) км/сек > VP,max » 8-10 км/сек (Викулин, Чернобай, 1986).
При DL » R0 (l = 4R0) минимальная оценка энергии взаимодействия, определяемая из соотношения (2.4.20), составляет Wint,min ~ 1016¸17 дж. Как видим, параметры реальных очагов толчков-дуплетов близки параметрам рассмотренной выше модели двух взаимодействующих блоков. Поэтому фактические данные по сильнейшим землетрясениям-дуплетам, на наш взгляд, подтверждают теоретический вывод ротационной модели о существовании сильного взаимодействия с положительной (-p/2 < f < p/2) энергией.
На существование сильного взаимодействия с отрицательной (p/2 < f < 3/2p) энергией, по-видимому, указывают сейсмологические данные, например, для района центральных Курил протяженностью 250-300 км. Действительно, в пределах этого участка сейсмофокальной зоны, заключенного между оо. Симушир и Кетой, неперекрываясь могли бы разместиться 3-5 очагов сильнейших землетрясений. Однако в течение последних 200-250 лет в этом районе не было отмечено ни одного такого землетрясения (Новый каталог..., 1977) при их средней для окраины Тихого океана повторяемости в одном месте, равной одному событию в 100±50 лет (Викулин, 1994), табл. 1.1.1.
Таким образом, сейсмологические данные и данные о цунами, полученные на материале Камчатки и Японии в течение последних нескольких сотен-тысячи лет, достаточно убедительно доказали, что дальнодействие между сейсмофокальными блоками - очагами сильнейших землетрясений существует и количественно может быть описано с помощью модельных соотношений, полученных выше. Тем самым было показано, что ротационная модель, в принципе, позволяет рассчитывать взаимодействие сейсмофокальных блоков друг с другом.
Величины энергии и момента силы упругого поля, ответственного за взаимодействие блоков, при их достаточно больших размерах, как видно из данных, полученных выше, могут достигать больших значений. В этой связи представляет определенный интерес рассмотреть модель, состоящую из большого количества взаимодействующих блоков. Рассмотрим одномерную цепочку поворачивающихся (взаимодействующих) блоков, расположенную внутри твердого тела, вращающегося с угловой скоростью W. Будем полагать, что все блоки имеют форму шаров одинакового радиуса R0.
Рассмотрим случай, когда все блоки в цепочке движутся равномерно. Тогда в соответствии с результатами, полученными выше, уравнение движения для блока в цепочке можно записать в виде:
Id2b/dt2 = K1 + K2 (2.4.26)
где b - как и выше, угол, на который повернулся блок, I = 8/15prR05 - его момент инерции, K1 - момент силы поля упругих напряжений, появляющегося вокруг блока в результате его поворота, значение которого определяется соотношением (2.4.12), K2 - момент силы, отвечающий за взаимодействие рассматриваемого блока с остальными блоками цепочки.
Из самых общих соображений ясно, что величина момента K2 должна быть пропорциональна как упругой энергии рассматриваемого блока, равного Vd2b/dx2, так и упругой энергии, соответствующей всем остальным блокам цепочки. В качестве последней выбираем величину, равную средней линейной плотности упругой энергии цепочки блоков w. Здесь V=4/3pR03 - объем блока, x - координата вдоль цепочки. Таким образом, момент силы, отвечающий за взаимодействие рассматриваемого блока с другими блоками цепочки, можно записать в виде:
K2 = zwVd2b/dx2 (2.4.27)
где z - безразмерный коэффициент, характеризующий «однородность» цепочки, т.е. в случае нашей задачи можно положить z = 1.
Окончательно, уравнение движения (2.4.26) для блока с координатой z в момент времени t с учетом (2.4.12) и (2.4.27) можно записать в следующем виде: ¶2q/¶x2 - c02¶2q/¶t2 = k02sinq, или в безразмерных координатах x = k0x, h = c0k0t:
¶2q/¶x2 - ¶2q/¶h2 = sinq (2.4.28)
где q = b/2,
![]() (2.4.29)
(2.4.29)
![]() (2.4.30)
(2.4.30)
Здесь, как и принято выше, V=4/3pR03 - объем блока, I=8/15prR05 - его момент инерции и w - линейная плотность выделяемой в цепочке упругой энергии.
Уравнение (2.4.28) известно как уравнение синус-Гордона (СГ). Решением этого уравнения (Скот, Чжу, Макфлин, 1973; Филиппов, 1990) являются локализованные волны - солитоны:
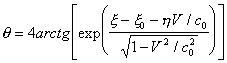 (2.4.31)
(2.4.31)
где x0 - центр солитона, V - его скорость.
Выражение для предельной скорости солитонов с0 может быть записано в виде:
с02 = 5/2wr-1R0-2 (2.4.32)
Отметим, что величина характерного периода процесса не является функцией линейной плотности выделяемой упругой энергии:
T = k0/c0 ¹ f(w) (2.4.33)
В длинной цепочке блоков, когда можно не учитывать влияние ее концов, возможны решения, получившие название экситонов (exitons) (Давыдов, 1982).
Качественная зависимость энергии возбуждений от скорости распространения для солитонов (I) и экситонов (II) приведена на рис. 2.4.3, взятом из работы (Давыдов, 1982). При этом зависимости для энергий возбуждений удовлетворяют следующим условиям:
Es ~ Vn1, Eex ~ Vn2, n1 > n2 (2.4.34)
В квазилинейном приближении, когда процесс можно описать с помощью линеаризованного уравнения СГ, закон дисперсии для экситонных решений записывается в виде (Филиппов, 1990):
w2 = w02(1 + l02/l2) (2.4.35)
где w и l - соответственно частота и длина волны экситона,
l0 = 2pс0/w0 (2.4.36)
w0 – «собственная» частота поворотного движения блока, l0 - соответствующая ей длина волны.
Первой отличительной особенностью закона дисперсии (2.4.35) является то, что частота распространяющихся по цепочке блоков волн всегда выше w0. Физически очевидно, что частота w0 достигается при большой длине волны (в пределе l ® ¥), когда все блоки цепочки движутся как единое целое, без ее деформации.
Второй характерной особенностью закона дисперсии (2.4.35) является его связь с нелинейными свойствами цепочки блоков, а не с ее дискретной структурой (Филиппов, 1990).
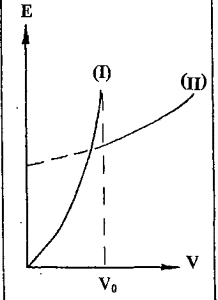
Рис. 2.4.3. Волновые решения уравнения СГ: I - солитоны, II - экситоны, V0 - характерная скорость процесса (Давыдов, 1982).
Групповая скорость экситонов, являющихся решением уравнения СГ (2.4.28), равна U = c02[1 + (k0/k)2]-1/2 и изменяется в пределах 0 £ U £ c0.
По аналогии с обычными упругими волнами примем, что длина волны экситона l0 равна размеру «элементарного» сейсмофокального блока:
l0 » R0, k0 = 2p/R0 (2.4.37)
для значения характерной скорости процесса с0 получаем следующее выражение:
![]() ~ VRVS
(2.4.38)
~ VRVS
(2.4.38)
Как видим, значение с0 может быть представлено в виде среднегеометрического произведения двух скоростей: центробежной VR = WR0 и упругой поперечной VS = (G/r)1/2.
При параметрах модели (2.4.16) для скорости с0 из (2.4.38) получаем занчение:
с0 » 1 см/сек (2.4.39)
Известный фактический материал по скоростям миграции сейсмичности вдоль тихоокеанской сейсмофокальной зоны собран в Приложении 2, табл. П.2.1, П.2.2 и представлен на рис. 2.4.4. Из данных этого рисунка видно, что все поле скоростей достаточно отчетливо разбивается на две области, разделенные значением:
V0 = (102 - 103) км/год » 1 см/сек (2.4.40)
В области с большими значениями (V2 > V0) расположены скорости миграции форшоков и афтершоков в очагах землетрясений (локальная миграция), в области с меньшими значениями (V1 < V0) - скорости, определяющие миграцию в больших пространственно-временных пределах (глобальная миграция).
С использованием представленных на рис. 2.4.4 данных методом наименьших квадратов в пределах каждой из выше обозначенных областей были рассчитаны следующие зависимости:
М0,1(±1,2) = (2,6±0,5)×lgV1 + (1,9±0,8), V1 < V0 (2.4.41)
M0,2(±1,2) = (1,3±0,3)×lgV2 - (2,5±1,6), V2 > V0 (2.4.42)
где М0 - наименьшее
значение магнитуды землетрясения в
анализируемых выборках сейсмических
событий. Полученные зависимости
практически не отличаются от таких же
зависимостей, полученных нами раньше (Викулин,
Иванчин, 1998) с использованием гораздо
меньшего (примерно в два раза) по объему
исходного материала по скоростям миграции
тихоокеанской сейсмичности.
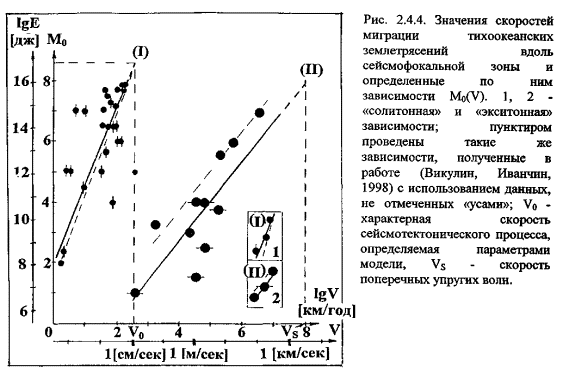
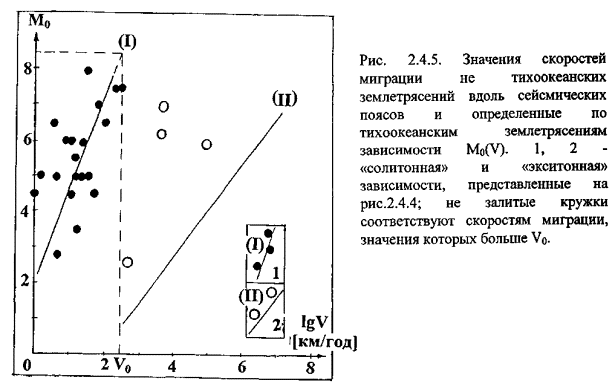
Отметим, что вывод о пропорциональности скорости миграции землетрясений значениям их магнитуд независимо был также сформулирован в работе (Wood, Allen, 1973) на материале о землетрясениях Сан-Андреаса.
Полагая, что магнитуда землетрясения с величиной упругой энергии Е, сбрасываемой при сейсмических толчках, определяется соотношением Гутенберга-Рихтера lgE,дж = 1,8М + 4,3, зависимости (2.4.41) и (2.4.42) можно переписать следующим образом
E1 » V15, V1 < V0 (2.4.43)
E2 » V22, V2 > V0 (2.4.44)
Видим, что V0, по сути, является предельной максимальной скоростью для первого решения (2.4.41). Более того, это значение, согласно (2.4.39), при принятых выше параметрах модельных величин близко характерной модельной скорости процесса:
V0 » с0 (2.4.45)
Соотношения (2.4.43) и (2.4.44), качественно являясь достаточно близкими аналогичным «солитонной» и «экситонной» зависимостям (см. рис. 2.4.3 и соотношения 2.4.34), представляют собою решения модельного уравнения синус-Гордона (2.4.28). При этом, солитонам соответствуют глобальные волны миграции со скоростями V1 < c0, экситонам - локальные (очаговые) волны со скоростями V2 > c0 (Давыдов, 1976).
Данные о скоростях миграции сейсмичности в пределах всех других регионов, расположенных вне тихоокеанской окраины, собраны в Приложении 2, табл. П.2.3 и представлены на рис. 2.4.5. Видно, что, в целом, они соответствуют полученным на материале тихоокеанских данных закономерностям (2.4.41) и (2.4.42).
Таким образом, показано, что значения скоростей миграции планетарной сейсмичности расположены в пределах двух непересекающихся областей. В пределах каждой области, значения могут быть описаны такими зависимостями, которые соответствуют распространяющимся на глобальные и локальные (в пределах очагов землетрясений) расстояния волны, являющиеся решениями модельного ротационного уравнения (2.4.28). И такой волновой способ описания сейсмического процесса, как показывают полученные результаты, может быть применимы для любого протяженного сейсмоактивного пояса планеты.
Разрыв в очагах сильных
землетрясений часто носит мультиплетный
характер. Все наиболее сильные последние
землетрясения планеты в 1952-1965 гг., очаги
которых имели протяженность многие сотни-тысяча
километров, представляют собою мультиплеты
(Wyss, Brune, 1967; Plafker, Savage, 1970; Wu, Kanamori, 1973; Иванов,
Гардер, 1985; Викулин, Чернобай, 1986 а,б; Иванов,
Константинова, 1988). Оказалось, что скорость
миграции толчков в мультиплете не зависит
от магнитуды землетрясения и равна
![]() » 3 ± 1 км/сек (табл. П.2.4). Наблюдаемые
экспериментально скорости скольжения
перед разрушением в образцах гранитов в
зависимости от приложенной нагрузки лежат
в тех же пределах и составляют 0,7-4,0 км/сек (Ohnaka,
Kuwahara, Yamamoto, 1987). Таким образом, скорость
миграции толчков в мультиплете, по сути,
является скоростью, в физике трещин
названной скоростью «вспарывания»,
значение которой близко поперечной
скорости звука VS.
С другой стороны, экстраполяция «экситонной»
зависимости (2.4.42) в область предельных
магнитуд M0 ® Mmax ³
8 (рис. 2.4.4) для скорости миграции дает
близкое значение, равное:
» 3 ± 1 км/сек (табл. П.2.4). Наблюдаемые
экспериментально скорости скольжения
перед разрушением в образцах гранитов в
зависимости от приложенной нагрузки лежат
в тех же пределах и составляют 0,7-4,0 км/сек (Ohnaka,
Kuwahara, Yamamoto, 1987). Таким образом, скорость
миграции толчков в мультиплете, по сути,
является скоростью, в физике трещин
названной скоростью «вспарывания»,
значение которой близко поперечной
скорости звука VS.
С другой стороны, экстраполяция «экситонной»
зависимости (2.4.42) в область предельных
магнитуд M0 ® Mmax ³
8 (рис. 2.4.4) для скорости миграции дает
близкое значение, равное:
Vex,max (M0 ® Mmax) » 108 км/год » 5 км/сек (2.4.45)
Значение для скорости миграции афтершоков с М ³ М0 = 5, составляющее » 1 км/сек, было отмечено в очаге Кроноцкого землетрясения 5.12.1997, М = 7,5-7,7 (Камчатка) сразу после главного толчка (Викулин, Сенюков, 1998).
Таким образом, полученные данные позволяют сделать вывод о том, что скорость вспарывания, являясь наибольшей скоростью миграции форшоков и афтершоков в очагах землетрясений, в рамках ротационной модели представляет собою предельно допустимое значение для скорости экситонной волны.
Данные, полученные в работах (Жадин, 1984; Андронов, Жадин, Поташников, 1989), убедительно показывают, что пространственно-временная структура миграции землетрясений в тектонических поясах имеет планетарную природу и указывает на существование прямой связи между сейсмическим процессом, с одной стороны, и мантийной конвекцией - с другой. Такой результат, с точки зрения тектоники плит, очевидно, равносилен выводу о том, что волны миграции сейсмичности имеют тектоническую природу и их закономерности, в том числе и выявленные выше в настоящей работе, должны определяться особенностями движения плит вдоль поверхности планеты.
Данные о движениях земной коры и сопровождавших их сейсмических явлениях собраны в Приложении 2. Из данных, представленных в табл. П.2.5, видно, что величина скорости волнового движения земной коры пропорциональна магнитуде, сопровождавшего это движение сейсмического явления. Также как и в случае миграции сейсмичности (рис. 2.4.4 и 2.4.5), скорости значением, близким V0, разделяются на две области. При этом в области малых значений скоростей (V < V0) достаточно уверенно выявляется зависимость, близкая солитонной (2.4.41).
В работах (Elsasser, 1969; Savage, 1971; Лобковский, Баранов, 1984) показано, что в процессе субдукции в зоне перехода от океана к материкам генерируются возмущения тектонического характера (волны тектонических напряжений), которые распространяются вдоль сейсмофокальной зоны со скоростями, характерными для глобальной миграции. Согласно данным работ (Маламуд, Николаевский, 1984; Николаевский, 1996), такими возмущениями являются уединенные волны с характерной длиной, составляющей первые сотни километров при физически оправданных значениях скорости ее распространения по порядку величины равных 10-1000 км/год. Они объяснялись колебаниями литосферной плиты на астеносферном потоке. По-видимому, к такому типу волн следует отнести возмущения «тектонических напряжений», распространявшиеся в течение ускоренного вращения Земли в 1978-1981 гг. вдоль Евразийской плиты со скоростью 2000 км/год » 1-10 см/сек (Сапрыгин, Василенко, Соловьев, 1997). Как видим, имеющаяся совокупность данных и проведенный в рамках тектонических моделей теоретический анализ позволяют сделать вывод о том, что солитонная ветвь решений модельного уравнения, описывающая волны миграции сейсмичности и деформации, действительно имеет тектоническую природу.
Имеются достаточно убедительные данные и о существовании соответствующей экситонной зависимости. На существование такой зависимости указывает, например, более «быстрая» волна (Sauers, 1986), которая в марте-мае 1986 г. распространялась вдоль Алеутских островов со скоростью 2×104 км/год » 1 м/сек и сопровождалась началами достаточно сильных извержений трех вулканов и землетрясением с магнитудой М=7,7 (№24, табл. П.2.5).
На камчатском геодинамическом полигоне с использованием светодальномера СГ-3, работающего с частотой опроса один раз в пять минут, в нескольких случаях удалось зарегистрировать кратковременные изменения (уменьшение) длин некоторых базовых линий протяженностью 5-20 км. В трех случаях такие изменения длин были вызваны местными землетрясениями, ощущавшимися на территории Камчатки с интенсивностью 4-8 баллов (Бахтиаров, Левин, 1991, 1993). При этом, продолжительность «бухтообразного» уменьшения длин составила примерно 20 минут для двух землетрясений в 1987 г. с М=5,3 и 5,6 на гипоцентральном расстоянии 110 км и несколько часов для Хаилинского землетрясения 8.3.1991 г. с М=7,0 на гипоцентральном расстоянии 1050 км. В случае землетрясения с М=7,0 в результате одновременного измерения длин двух базовых линий, по-видимому, впервые удалось определить и скорость «быстрой», по сути «экситонной», волны деформации, значение которой составило 105 км/год » (1-10) м/сек (табл.П.2.5, №17).
Таким образом, проведенная выше в рамках ротационной модели интерпретация полученных решений в виде солитонов и экситонов и физически и сейсмологически может считаться обоснованной. При этом, связанные с относительным движением плит (Elsasser, 1969), с изгибом пододвигаемой под материк плиты (Николаевский, 1996) или с другими причинами (Savage, 1971), тектонические силы, генерирующие волны миграции сейсмичности со скоростями V < c0, могут быть смоделированы в рамках развиваемой в настоящей работе ротационной модели сейсмического процесса. Экситонный характер «быстрых» (с V > c0) тектонических и деформационных волн в данной работе установлен впервые.
Следует отметить, что и «солитонный» и «экситонный» характер решений уравнения СГ определяется такой его особенностью, физика которой заключается во взаимном уравновешивании эффектов нелинейности среды и дисперсии волн. Именно такого рода решения выявлены в большом количестве задач из разных областей физики (Скотт, Чжу, Макфлин, 1973) и в том числе в таких задачах физики твердого тела как распространение дислокаций в кристаллах (Филиппов, 1990) и волновые возмущения в квазиодномерных молекулярных структурах (Давыдов, 1982). Далее, полученные в последнее время экспериментальные данные позволили установить существование как нелинейных свойств у земной коры (Проблемы..., 1987), так и дисперсии у сейсмических волн (Барабанов и др., 1988; Касахара, 1985, с.208; Нерсесов и др., 1990) и, как следствие, солитонных свойств у волновых сейсмических полей (Проблемы..., 1987). Примеры сейсмотектонических задач, для которых установлены «солитонные» решения, приведены в обзоре работы (Быков, 2000 а).
Земля испытывает свободную прецессию. В геофизической литературе ее обычно называют свободной нутацией Эйлера, или по имени ее первооткрывателя в 1891 г. - чандлеровское колебание полюса. Такие колебания возникают вследствие того, что ось вращения Земли слегка наклонена к оси наибольшего момента инерции. Полный момент количества движения планеты остается постоянным и по величине, и по направлению, а Земля движется так, что полюс описывает на ее поверхности круг с центром в точке пересечения оси наибольшего момента инерции с поверхностью Земли. Ось вращения Земли практически фиксирована в пространстве и чандлеровские колебания полюса выражаются в периодических вариациях широты с периодом 430-435 суток и переменной амплитудой, составляющей, в среднем, 0//,14 (Манк, Макдональд, 1964). Прецессия полюса происходит в сторону, обратную вращению Земли.
Согласно (Манк, Макдональд, 1964) существует два вопроса, по которым исследователи к настоящему времени не пришли к полному согласию: 1) Какова ширина чандлеровской полосы? 2) Существует ли вековое изменение средней широты? В свете последних данных вторую проблему можно считать решенной: вековое изменение средней широты происходит со скоростью около 0//,003 в год в направлении 70-80оW.
Дискуссионной является и сама проблема возбуждения и затухания чандлеровских колебаний. Большинство исследователей считают, что требуемая добротность чандлеровских колебаний может быть обеспечена за счет процессов, протекающих в ядре и мантии (Манк, Макдональд, 1964; Магницкий, 1965). Согласно (Молоденский, 1953; Парийский, 1963; Магницкий, 1965), данные по колебаниям Чандлера подтверждают и уточняют модель Земли с жидким ядром. В работе (Авсюк, 1996) показывается, что энергетика чандлеровских колебаний может быть объяснена движениями твердого ядра Земли, вызываемыми возмущениями в системе Солнце-Земля-Луна. Однако, обосновать конкретный механизм, использующий взаимосвязь такого рода, будет достаточно сложно по «частотным» соображениям: величина периода такого движения ядра на несколько порядков превышает период чандлеровских колебаний. Некоторые исследователи полагают, что эта проблема не может быть решена за счет процессов, протекающих в мантии (Rochester, Smylie, 1965), атмосфере (Munk, Hassan, 1961) и магнитосфере (Стейси, 1972). Более того, согласно (Стейси, 1972), механизм возбуждения и затухания колебаний полюса до сих пор остается невыясненным. По-видимому, по этой причине в литературе, насколько нам известно, не обсуждался вопрос о взаимосвязи нутации полюса с другими собственными колебаниями планеты.
Пожалуй, у большинства исследователей не вызывает сомнений вопрос о том, что колебания Чандлера «определяются внутренним (по отношению к Земле - авт.) перераспределением момента количества движения; внешние воздействия несущественны» (Стейси, 1972).
В качестве основы одной из возможных моделей, с помощью которой можно было бы объяснить возбуждение чандлеровских колебаний, как и других собственных колебаний планеты, неоднократно предлагалось использовать процессы в очагах сильных землетрясений (Манк, Макдональд, 1964; Стейси, 1972; Chao, Gross, 1995). По-видимому, априори предполагая существование тесной взаимосвязи между этими планетарными явлениями, в атласе (Котляр, Ким, 1994) на графическом представлении временных рядов вариаций параметров вращения Земли нанесены и сильные сейсмические события.
В соответствии с данными работ (Манк, Макдональд, 1964; Стейси, 1972; Котляр, Ким, 1994; Курбасова и др., 1997) в настоящее время вопрос о существовании взаимосвязи между сейсмичностью и свободной прецессией полюса Земли также можно считать дискуссионным. Действительно, с одной стороны гипотезы о существовании взаимосвязи между такими планетарными процессами в течение последних десятилетий неоднократно предлагались различными исследователями. Однако, последующие исследования и расчеты, выполненные в рамках известных модельных представлений, их не подтверждали (Манк, Макдональд, 1964; Стейси, 1972). С другой стороны, анализ, проведенный в (Курбасова и др., 1997), позволил авторам сделать предположение о возможности синхронизации вариаций с 10-летним периодом в геодинамических и гелеофизических процессах. Согласно данных, приведенных во введении к атласу (Котляр, Ким, 1994), имеет место «короткоинтервальная корреляция землетрясений с опережающими их девиациями показателей вращения» планеты при «триггерной модели взаимосвязи сейсмических событий с ротационными» процессами.
На наш взгляд, такой на первый взгляд противоречивый ход событий может являться следствием того, что имеет место дефицит механических моделей, описывающих сейсмичность как динамический процесс планетарного масштаба.
Следует отметить, что в науках о Земле проблема колебаний Чандлера, как и проблема вращения Земли вообще, является не просто важной, но фундаментальной. По мнению авторов (Манк, Макдональд, 1964) «Разнообразие предмета чудовищно. Он затрагивает все разделы геофизики». В частности, исследуя колебания Чандлера и возбуждающие их механизмы, можно уточнять геофизические параметры процессов, протекающих в пределах, как всей Земли, так и отдельно взятых ее частей. Проблема чандлеровских колебаний, кроме того, является весьма поучительной и с точки зрения корректности ведения научной дискуссии, имевшей место на рубеже XIX-XX вв. и в последующие годы (Авсюк, 1996).
В последние годы нами разработана ротационная модель сейсмического процесса (Викулин, 1990; Викулин, Иванчин, 1998). В рамках такой модели сейсмофокальный объем, протягивающийся вдоль окраины Тихого океана, являющейся самым сейсмически активным в ХХ столетии поясом планеты, имеет широкий спектр собственных колебаний (Викулин, 1992,1997). Ниже показывается, что определенный частотный диапазон этого спектра приходится на чандлеровские колебания, которые, таким образом, вызываются изменением формы Земли вследствие тектонического процесса, протекающего в пределах сейсмически активных поясов планеты (Викулин, 2000; Викулин, Кролевец, 2001).
Экспериментальные определения положения полюса планеты начались в 1846 г. Все накопленные включительно до 1989 г. данные содержатся в двух обстоятельных монографиях (Котляр, Ким, 1994; Курбасова и др., 1997). Эти данные представлены мгновенными значениями координат оси вращения планеты.
Данные за 1846-1969 гг. представлены в работе (Федоров и др., 1972). Данные за 1846-1889 гг., характеризующиеся дискретностью 0,1 года, получены на трех обсерваториях и имеют точность 0//,08-0//,09, точность данных за 1890-1969 гг. по данным пяти станций Международной службы широты с дискретностью 0,05 года не лучше 0//,03-0//,04. Данные в (Федоров и др., 1972) за весь период наблюдений представлены в единой системе среднего полюса эпохи.
В атласе (Котляр, Ким, 1994) представлены данные за 1897-1989 гг., как и в (Федоров и др., 1972), с дискретностью 0,05 года. Их точность в периоды 1962-1979 гг., 1980-1983 гг. и в 1984 г. и в последующие годы составляет 0//,010-0//,015, около 0//,001 и лучше 0//,0002. Однако, в отличие от (Федоров и др., 1972), данные в (Котляр, Ким, 1994) за разные интервалы наблюдений представлены в разных системах координат. Для их совмещения, начиная с 1903 г. необходимо использовать поправки, величины которых для разных лет различны (Котляр, Ким, 1994).
Приведенные данные показывают, что наиболее однородным материалом, который в течение продолжительного отрезка времени характеризует движение полюса в единой системе координат, являются данные за 1890-1969 гг., приведенные в (Федоров и др., 1972). Данные за этот период наблюдений, в основном, и использовались нами в настоящей работе. Они представлены 1581 парой значений мгновенных координат оси вращения Земли. Существует современная переработка результатов наблюдений широт на станциях Международной службы широты. Однако, в рамках данной работы их отличие от данных в (Федоров и др., 1972) несущественно.
Данные за 1890-1969 гг. приведены на рис. 2.5.1 а. На этом рисунке ось ОX направлена по гринвичскому меридиану, а ось OY - в восточном направлении. Начало системы координат (О) расположено в точке, соответствующей положению среднего полюса в течение всей эпохи наблюдений. Данные за короткие отрезки времени, демонстрирующие основные виды траекторий движения полюса, приведены на рис. 2.5.1 b, c, d. Видно, что практически в течение всего исследуемого периода наблюдений движение полюса происходит вдоль достаточно гладких траекторий, имеющих формы «раскручивающихся» или «закручивающихся» окружностей, эллипсов или овалов в сторону, обратную вращению Земли (рис. 2.5.1 а, d). Такое направление, вслед за (Манк, Макдональд, 1964), будем считать положительным, движение в обратном направлении - отрицательным. В течение некоторых достаточно непродолжительных отрезков времени траектория движения полюса планеты имеет «изломы» (рис. 2.5.1 c) или даже направлена в отрицательном направлении (рис. 2.5.1 b). Более подробно динамику изменения траекторий движения полюса планеты можно проследить, например, с помощью графического материала в (Котляр, Ким, 1994), представленного данными, охватывающими последовательные 1-2 летние интервалы наблюдений.
Из данных, приведенных в работах (Федоров и др., 1972; Котляр, Ким, 1994), видно, что все траектории движения полюса в 1890-1989 гг. заключены в пределах круговой площадки с радиусом Dach,max » 0//,40 » 12,3 м » 2´10-6 рад. Этот радиус можно считать максимальным значением амплитуды колебаний полюса планеты в течение всего периода наблюдений в 1846-1989 гг. При этом, как уже отмечалось выше, долговременное среднее значение амплитуды колебаний полюса планеты (колебаний Чандлера) составляет Dach,ср » 0//,14 » 4,3 м » 7´10-7 рад.
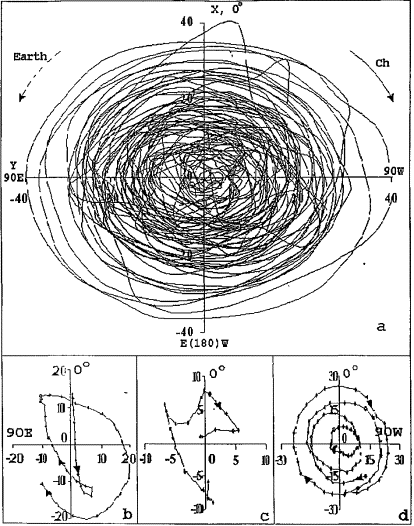
Рис. 2.5.1. Траектории нутации полюса планеты, построенные по данным за 1890-1969 гг. (а) и периодов 1895-1896 гг. (b), 1926 г. (с) и 1960-1964 гг. (d). Значение амплитуды колебаний приведено в сотых долях угловой секунды; стрелками показано направление нутации (Ch), пунктирной стрелкой - направление вращения Земли (Earth). Оси ОХ и ОY направлены вдоль Гринвичского и 90Е меридианов соответственно.
Спектр колебаний широты, полученный по наблюдениям в течение 1891-1945 гг. с дискретностью данных 0,1 года, представлен в (Манк, Макдональд, 1964). Из данных этой работы авторами сделаны следующие выводы.
1) Подавляющая часть всей энергии (» 99%) приходится на колебания, происходящие в положительном направлении (на колебания с положительными частотами),
2) Большая часть энергии (около 90%) колебаний приходится на два диапазона частот. Первый заключен в пределах чандлеровской полосы частот, «центрированной» на значение fch = 0,85 год-1 (Тсh = 430 суток » 1,2 года) и имеющей заметную полосчатую структуру, представленную одним главным и двумя (примерно на порядок меньшими по амплитуде) боковыми максимумами; второй - представлен годовой гармоникой f1 = 1 год-1 (Т1 = 1 год).
В рамках ротационной модели было показано существование решения, закон дисперсии которого (2.4.35) допускает колебание всей цепочки взаимодействующих сейсмофокальных блоков, как целой. Частота таких «нулевых» колебаний w0 и их скорость с0 определяются соотношениями (2.4.35)-(2.4.39).
В рамках ротационной модели закон дисперсии (2.4.35) объясняется сильными нелинейными свойствами цепочки блоков - их дальнодействующим взаимодействием друг с другом, что приводит к существованию моды с частотой w0, реализующейся при большой длине волны (в пределе l®¥), когда все блоки цепочки движутся как единое целое, без ее деформации. При этом пружины, моделирующие взаимодействие блоков друг с другом, настолько слабо должны деформироваться, что их как бы и не должно быть вовсе. Такое движение соответствует повороту всего сейсмофокального объема тихоокеанского кольца, как целого, в плоскостях, перпендикулярных сечению кольца, когда l ® ¥ равносильно l ® L, где L » 4×104 км - протяженность кольца.
Такое вращательное движение сейсмофокального кольца, расположенного в пределах переходной зоны и упруго связанного как с тихоокеанской так и с окружающими ее материковыми плитами, очевидно, должно сопровождаться вертикальными (относительно поверхности Земли) колебаниями некого объема тороидальной формы и, следовательно, вследствие изменения формы Земли должно приводить к прецессии полюса планеты с частотой wо (Викулин, 1997).
Покажем, что прецессия полюса с «нулевой» частотой wо и является колебаниями, соответствующими максимуму на частоте Чандлера fch.
Будем считать, что 1) Параметры колеблющейся кольцевой области одинаковы на всем ее протяжении вдоль окраины Тихого океана. 2) Кольцевая область имеет тородоидальную форму и расположена в плоскости кольца, имеющего субмеридиональное простирание. 3) Кольцо расположено на расстоянии R^=Rзcosj от центра Земли, Rз - ее радиус, j » 50о - половина угла, под которым кольцо «видно» из центра Земли: вдоль меридиана - от Алеутских островов - Аляски, j=50-60оN на севере до линии, соединяющей о. Веллингтон (j=50оS, l=75oW) с островами Окленд (j=60oS, l=170oE) на юге; вдоль экватора - от Соломоновых островов (l=160оЕ) на востоке до Центральной Америки (l=80oW) на западе. Тогда изменение момента инерции Земли вследствие таких колебаний составит DI = D(R^2m) = 2R^dm = 2Rзdmcosj, где d = dH - амплитуда колебаний кольцевого объема с вертикальным размером H, m - масса колеблющегося объема.
Имеющиеся сейсмологические (с) данные позволяют определить период «нулевых» колебаний сейсмофокального кольца. При протяженности элементарного сейсмофокального блока Lo = 150-300 км » 250 км и предельном значении скорости таких волн со » 200 км/год (Николаевский 1996; Викулин, 1997) для периода нулевых колебаний всего кольца как целого из соотношений (2.4.33) - (2.4.39) получаем To,с » 1,2 года.
Согласно геодезическим (г) данным, полученным на геодинамическом полигоне вблизи Петропавловска-Камчатского в течение непрерывных наблюдений, проводимых уже более двадцати лет (Бахтиаров, Левин, 1991), изменение длин базовых линий li происходит с характерным периодом Тг = 1-1,5 года при амплитуде изменения длин линий dг = Dli/li =(1¸5)×10-6 » 3×10-6.
Петропавловск-Камчатский расположен в непосредственной близости от сейсмофокального объема. Удаление базовых линий от города не превышает 100 км. Поэтому полученные в работе (Бахтиаров, Левин, 1991) геодезические данные указывают на то, что амплитуда вертикальных колебаний сейсмофокального объема и прилегающей к нему части вблизи Камчатки с периодом Тг, по всей видимости, имеет тот же порядок величины. Тогда полагая, что сечение колеблющегося кольцевого объема тороидальной формы составляет H×D » (300¸400)×(300¸400) км2, m=rHDL, r»3 г/см3- плотность, d » dг, для величины изменения момента инерции Земли получим значение DIг = 1036 - 1037 г×см2, что, в свою очередь, согласно (Стейси, 1972), должно вызвать нутацию полюса с периодом Тг и с амплитудой Daг = DI/(С - А) » 10-6 рад. Здесь: С - А = 2,6×1042 г×см2 - разность между полярным и экваториальным моментами инерции Земли.
Таким образом, проведенный анализ показал, что значения модельных и экспериментально измеренных величин близки параметрам, характеризующим колебания Чандлера: Тo,с » Тг » Тch, Daг » Dach. Как видим, «нулевые» колебания окраины Тихого океана, имеющие сейсмотектоническую природу, могут рассматриваться в качестве возможной причины, приводящей к нутации полюса Земли на частоте Чандлера. Другими словами, в рамках ротационной модели сейсмического процесса чандлеровское колебание полюса следует считать в большей степени взаимосвязаными с процессами взаимодействия сейсмофокальных блоков в цепочке, чем с процессами в очаге отдельно взятого землетрясения пусть даже с предельной магнитудой и протяженным очагом.
Тихоокеанская окраина является
не единственным сейсмическим поясом
планеты. Вторым по интенсивности и
протяженности является Альпийско-Гималайский
сейсмический пояс, в субширотном
направлении протянувшийся вдоль
поверхности Земли примерно на 150о (Шейдегер,
1987). Уровень сейсмической активности вдоль
этого пояса значительно ниже активности
тихоокеанского кольца. Однако, как следует
из ротационной модели, значение периода «нулевых»
колебаний сейсмотектонического процесса,
определяемого из соотношений (2.4.29)-(2.4.30), не
зависит от линейной плотности упругой
энергии в поясе
(2.4.33): Т0 = k0/c0
¹ f(W). Далее, нетрудно показать,
что амплитуда нутации полюса планеты,
которая могла бы быть вызвана «нулевыми»
сейсмотектоническими движениями в
пределах Альпийско-Гималайского пояса, при
тех же параметрах колеблющегося объема по
порядку величины совпадает с той, которая,
как было показано выше, генерируется, по
сути, такими же движениями тихоокеанского
пояса. На основании этих данных в рамках
ротационной модели можно предложить
гипотезу, согласно которой чандлеровский
максимум должен быть представлен двумя «нулевыми»
частотами, каждая из которых соответствует
процессу, протекающему в пределах
тихоокеанского или альпийско-гималайского
пояса. При этом, в соответствии с эффектом
Доплера «нулевая» частота
w0,а-г, отвечающая альпийско-гималайскому
поясу, вследствие его субширотного
простирания, должна соотноситься с такой же
частотой w0,т-о
для тихоокеанского пояса, имеющего, в
основном, субдолготное простирание,
следующим образом:
![]() , где V = RзW
= 0,465 км/сек - линейная скорость движения
поверхности планеты в районе экватора, W -угловая скорость ее вращения, Rз
- радиус Земли, Vкр - скорость
крутильных колебаний, которые, как будет
показано ниже (см. раздел 3.1), ответственны
за взаимодействие сейсмофокальных блоков
друг с другом, Vкр = (0,1 - 1)VS » 0,5VS (Ландау,
Лившиц, 1965), VS»4,4
км/сек - скорость поперечных волн в
литосфере.
, где V = RзW
= 0,465 км/сек - линейная скорость движения
поверхности планеты в районе экватора, W -угловая скорость ее вращения, Rз
- радиус Земли, Vкр - скорость
крутильных колебаний, которые, как будет
показано ниже (см. раздел 3.1), ответственны
за взаимодействие сейсмофокальных блоков
друг с другом, Vкр = (0,1 - 1)VS » 0,5VS (Ландау,
Лившиц, 1965), VS»4,4
км/сек - скорость поперечных волн в
литосфере.
Положение
полюса в каждый момент времени
определяется координатами точки на
плоскости XOY (рис. 2.5.1) или комплексным
числом z=x+iy. Другими
словами, вместо двух временных рядов {x} и {y}
действительных чисел нами рассматривался
один временной ряд комплексных чисел {z}.
Такой временной ряд может быть записан в
виде: ![]() , где N=1581 - полное число значений {z}, T=79,05 лет -
продолжительность интервала наблюдений
(1890-начало 1969 гг.), t - текущее время, в юлианских годах,
отсчитываемое от 1890 г, Сl-
коэффициенты гармоник с частотами fl
= l/T, l - целое число,
принимающее значения от - (N-1) до N-1. Как видим,
временной ряд {z} может быть однозначным
образом представлен в виде суммы гармоник Сlexp(i2pflt) с положительными и
отрицательными частотами. Здесь, как и в (Манк,
Макдональд, 1964), полагаем, что положительные
частоты описывают вращательное движение
полюса в положительном направлении (в
направлении от оси OX к оси OY), а
отрицательные - в противоположном
направлении. Коэффициенты гармоник Cl
вычислялись по формулам
, где N=1581 - полное число значений {z}, T=79,05 лет -
продолжительность интервала наблюдений
(1890-начало 1969 гг.), t - текущее время, в юлианских годах,
отсчитываемое от 1890 г, Сl-
коэффициенты гармоник с частотами fl
= l/T, l - целое число,
принимающее значения от - (N-1) до N-1. Как видим,
временной ряд {z} может быть однозначным
образом представлен в виде суммы гармоник Сlexp(i2pflt) с положительными и
отрицательными частотами. Здесь, как и в (Манк,
Макдональд, 1964), полагаем, что положительные
частоты описывают вращательное движение
полюса в положительном направлении (в
направлении от оси OX к оси OY), а
отрицательные - в противоположном
направлении. Коэффициенты гармоник Cl
вычислялись по формулам
![]()
Рассчитанный спектр нутации полюса планеты S = mod(Cl), измеряемый в сотых долях угловой секунды, как функция частот fl представлен на рис. 2.5.2 а. Из данных, представленных на этом рисунке, видно, что, как и в соответствии с данными предыдущих исследователей (Манк, Макдональд, 1964), движение полюса планеты, в основном, происходит в положительном направлении, и характерные частоты такого движения также заключены в пределах двух интервалов: в области чандлеровского максимума fch и годовой гармоники.
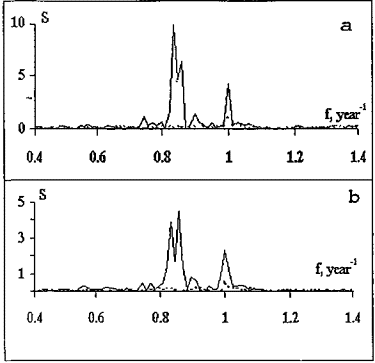
Рис. 2.5.2. Огибающие спектров для положительных и отрицательных (пунктиром) частот, построенные по данным за 1890-1969 гг. с помощью Фурье-анализа (а) и окна Флеминга (b). Спектральная плотность S выражена в сотых долях угловой секунды.
Движение полюса в области Чандлеровских колебаний, как видно из данных, представленных на рис. 2.5.2 а, характеризуется спектром, огибающая которого в области колебаний Чандлера имеет два максимума. Одному из них, большему по амплитуде, соответствует частота fch,1 = 0, 835 год-1 (Tch,1 = 437 дней), второму, меньшему - fch,2 = 0,860 год-1 (Tch,2 = 425 дней).
С целью проверки эффекта расщепления частоты Чандлера был проведен спектральный анализ с использованием окна Хэминга. Как видно из данных, представленных на рис.2.5.2 b, в этом случае эффект расщепления частоты Чандлера fch на две fch,1 и fch,2 стал еще более очевидным. При этом, амплитуды обоих частот fch,1,2 оказались примерно равными.
Таким образом, спектральный анализ показал, что нутация полюса на частоте Чандлера представлена двумя процессами с близкими частотами fch,1 и fch,2.
Покажем, что расположение тихоокеанского и альпийско-гималайского поясов соответствует особенностям распределения амплитуд «нулевых» колебаний на частотах fch,1 и fch,2, протекающих в их пределах сейсмотектонических процессов. Наличие такого соответствия можно пытаться установить, например, с помощью сравнительного анализа, при котором из исходного ряда значений {z} «исключается» та или иная гармоника. С этой целью проводилось построение полярных диаграмм. Для чего между всеми последовательными парами значений {xi, yi}, {xi+1, yi+1} определялись амплитуды и углы, характеризующие перемещение полюса в течение интервалов длительностью 0,05 года. Соответствующие полярные диаграммы строились для исходного ряда {z} (рис. 2.5.3 а) и для рядов {z1} (рис. 2.5.3 b) и {z2}(рис. 2.5.3 c), в которых исключались частоты fch,1 и fch,2 соответственно. При вычислении рядов {z1} и {z2} коэффициенты Сl, стоящие при «исключаемых» гармониках, полагались равными нулю.
Из данных, представленных на рис. 2.5.3, можно видеть, что гистограмма {z}, построенная по всей совокупности исходных данных (рис. 2.5.3 а), является «изотропной», т. е. не имеющей выделенных направлений, в то время как гистограммы с исключенными гармониками (рис. 2.5.3 b, c) такие направления имеют. Действительно, амплитуды отклонения оси вращения Земли имеют наибольшие значения на гистограмме {z1}(рис. 2.5.3 b) вдоль долготы I - 30oW-150oE (±20о) и на гистограмме {z2}(рис. 2.5.3 c) вдоль долготы II - 10oW-170oE (±10о). При этом угол g между азимутами I и II оказался близким углу b между направлениями на «центры тяжести» сейсмических поясов (1) и (2): g » b » 20о.
Равенство углов g » b, отражающее, с одной стороны, взаимное расположение поясов, и с другой - особенности движения полюса планеты, которые могли бы быть вызваны протекающими в этих поясах сейсмотектоническими процессами, нам представляется не случайным. Проведенный анализ, на наш взгляд, указывает на то, что особенности распределения амплитуды колебаний Чандлера по долготе связаны именно с особенностями сейсмотектонического процесса, протекающего в пределах тихоокеанского альпийско-гималайского поясов на частотах fch,1 и fch,2.
Как видим, данные анализа спектрального и пространственного (долготного) распределений подтверждают вывод ротационной модели о расщеплении чандлеровской частоты fch=0,85 год-1 на две fch,1=0,83 год-1 и fch,2=0,86 год-1, которые могут соответствовать «нулевым» частотам сейсмотектонических процессов, протекающих в пределах тихоокеанского и альпийско-гималайского поясов.
Сравнительный анализ (рис. 2.5.3) не позволяет каждому из поясов однозначным образом поставить в соответствие ту или иную из расщепленных частот. Однако в соответствии с требованиями, накладываемыми эффектом Доплера, можно принять, что частоты fch,1=0,83 год-1 и fch,2=0,86 год-1 соответствуют Тихоокеанскому и Альпийско-Гималайскому поясам соответственно.
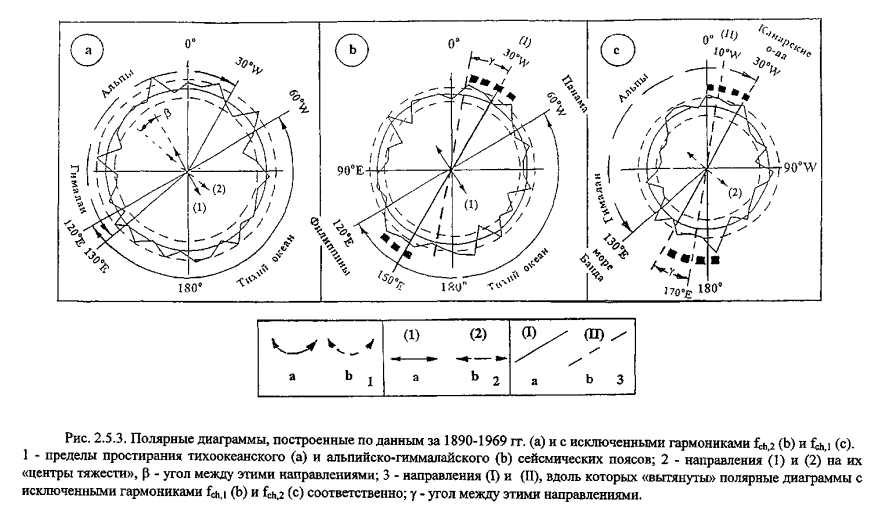
©IVGG 2003