Аннотация.
На основании использования разработанной
на основе учения о симметрии в рамках
концепции уровней организации и с учетом
динамической сущности пространства
технологии моделирования геодинамических
параметров тектоно-магматических систем в
связи с их рудоносностью выполнено
моделирование параметров золотоносной
Джалиндинской тектоно-магматической
системы (Соловьевский свод, Амуро-Охотская
складчатая система). Получены
аналитические зависимости, связывающие
состав и относительную
дифференцированность состава
магматических образований и оруденения с
вертикальными и горизонтальными размерами
тектонических образований в пределах свода,
и скоростями их деформирования. Сделан
вывод, что скорости деформирования,
пространственные размеры, состав
магматических пород и руд принимают
дискретные значения.
Согласно
закону соответствия определенным
тектоническим структурам сответствуют
вполне определенные магматические,
метаморфические, осадочные и рудные
формации (Щеглов, 1987). Формирование
месторождений, для случая связи оруденения
с магматизмом, может развиваться по трем
основным вариантам: а) перемещенные рудные
концентрации образуются в результате
магматической дифференциации без
существенного массообмена в областях их
отложения; б) формирование оруденения
происходит в результате взаимодействия
ювенильных и метеорных термальных вод с
горными породами в температурном поле
интрузива; в) рудные тела возникают
вследствие реализации вариантов “а” и “б”,
т.е в результате пространственного
совмещения разнородных процессов. В данной
статье, на примере золоторудной минерализации
жильного типа (для которой наиболее
вероятно формирование по первому варианту),
связанной с развитием Джалиндинской
тектоно-магматической системы,
локализованной в центральной части
Соловьевского свода, показываются
зависимости пространственно-временных
параметров тектонических структур с
составом магматических тел и ассоциирующим
оруденением.
Методика
Технология
моделирования геодинамических параметров
тектоно-магматических систем в связи с их
рудоносностью разработана на основе учения
о симметрии в рамках концепции уровней
организации, с учетом динамической
сущности пространства (Тишкин, 1996;1997). На
начальном этапе, методами
геоморфологического картирования с
применением материалов по дешифрированию
аэро-, космоснимков, выделяются
тектонические структуры различного
иерархического уровня, соответствующие
современному состоянию геолого-геофизического
пространства. Затем полученные результаты
сопоставляются с геологическими и
геофизическими данными, уточняются границы
структур на интересующий отрезок
исторического времени и, по необходимости (возможности),
заверяются полевыми наблюдениями. Далее, по
петрохимическим данным в выделенных
тектонических структурах определяется
структурно-химическое состояние
изверженных пород, выделяются
магматические комплексы и аналитическими
методами рассчитываются пространственно-временные
параметры тектоно-магматических систем для
различных уровней иерархии.
Для
удобства восприятия сути предлагаемой
работы приведем некоторые определения и
применяемые аналитические выражения с
необходимыми коментариями.
Граница (область
раздела) - часть пространства,
одновременно принадлежащая движущимся
смежным объектам и характеризующаяся
взаимодействием (суперпозицией)
элементарных ячеек рассматриваемых тел.
Тектоно-магматическая
система трактуется как состояние
логически ограниченного геологического
пространства, проявленное в синхронно
образованных формах магматических тел и
тектонических структур, относящихся к
одному структурному уровню (уровню
организации).
Геодинамическое
поле (ГДП) - все геодинамическое
пространство или логически ограниченная
его часть, характеризующаяся в момент
времени совокупностью силовых (энергетических)
полей, образующих ее элементарных ячеек
всех уровней организации.
Источником
геодинамического поля (ГДП) данного уровня
являются движущиеся элементарные ячейки (ЭЯ):
ядро, оболочки в системе “Земля”; слои
земной коры, мантии, и др. в системе “оболочка”;
тектонические блоки в оболочках и
подооболочках, комбинации которых образуют
структуры различных рангов; другие тела и
слагающие их отдельности: диапиры,
магматические расплавы, кристаллы,
молекулы, атомы и др.. ГДП служит
переносчиком взаимодействий между
различными ЭЯ по схеме ЭЯ-поле-ЭЯ. ГДП может
быть локальным - в границах ЭЯ и нелокальным
- в границах структур различных уровней.
Результирующая сила геодинамического поля
ГДП представляется в следующем виде:
F
= F1 + F2; F2
= f(V/U)
(1),
где F1 и F2
- перпендикулярно ориентированные силы,
совпадающие по направлению, соответственно,
с движением объекта и распространением (деформированием)
ГДП; V, U - соответственно, скорости движения
объекта и распространения ГДП.
Состав
магматических пород или их структурно-химическое
состояние выражается при помощи следующих
петрохимических модулей:
А = В + С
= (Еакт-а)/b =
100(STiO2,FeO,MgO,
CaO,MnO,H2O
/SSiO2,Al2O3,Fe2O3,P2O5)+
100(SK2O,Na2O/SSiO2,Al2O3,Fe2O3,P2O5),
где Еакт -
энергия активации вязкого течения; а, b -
эмпирические коэффициенты. В этих
координатах далее отстраиваются графики
структурно-химического состояния пород (V и
Z типов), позволяющие различать фазы
внедрения и магматические комплексы, т.е.
судить об однородности и постоянстве
геодинамического поля, в котором
формировались рассматриваемые ассоциации
пород.
Относительная
дифференцированность магматитов в системе
представляется в следующем виде:
L=tga=(Смакс-Смин)/(Амакс-Амин)=DС/DА
(макс. и мин., соответственно, максимальные и
минимальные значения).
Так
как L имеет физический смысл скорости, мы
вправе записать уравнение силы:
L
= (F×t)/(r×W)
(2),
где F - сила ГДП,
действующая на магматический очаг объема (W)
за время (t), r-
плотность вещества в очаге.
Размеры
очага (тектонической структуры) и скорость
его деформирования (U) связаны следующим
соотношением:
К = h/S
= a×(15.61
- U)×pm*
(3),
где h -
вертикальные размеры и S - площадь сечения
очага; а = 1.647×10-4
("линия Хонсю"); р = 2.154 - коэффициент
пропорциональности или подобия размеров
структур, являющийся членом геометрической
прогрессии pn= a0pn = a0(101/72)n
= a01.032497n (при а0 = 1 и n= ±0,1,2,3...);
в общем случае m* = ±
0,1,2...
Зависимости
относительной дифференцированности
магматитов со скоростью деформирования и
размерами структур приведены ниже:
L
= b×(15.76
- U)
(4),
где
b = 0.026.
L
= (S/10n)-2/3 (n
= ±0,1,2,3..)
(5).
L/K
= L×S/h
= (b/a)×pm*
= const×pm*
(6),
(const = 157.86 -
соответствует "линии Хонсю" при m=0;
константа получена при условии, что
элементы в скобках в правых частях
соотношений 3 и 4 равны). Число подобия
структур:
рm*
= p2n/pm
(7)
(m*-
целое число). Уравнение (6) хорошо описывает
изменение состава магматитов в
геодинамических системах различных
уровней иерархии.
hm
= S1/3 ×p2n/const×pm*×pm
(8).
Sm
= S1/3 ×
p2n/const×K×pm*×pm
(9),
Sm - площадь
структуры, соответствующая квантовому
уровню глубинности hm (вертикальной
дискретности) при данном значении К и рm*;
pm задает шаг изменения
пространственных размеров структуры.
Из
уравнений (3), (4) и (5) и с учетом динамической
природы границ можно полагать, что число n
отражает величину силы взаимодействия
движущегося объекта (магматического
расплава) с вмещающей локальной структурой
(геодинамическим полем) - чем больше n, тем
больше сила взаимодействия. Величина же
числа m показывает глубинный уровень
активизации внешней структуры, с развитием
которого связано формирование данного
объекта в локальной тектонической
структуре, отражая величину силы
взаимодействия рассматриваемой структуры
с внешней структурой более высокого ранга.
Число m*
является коэффициентом подобия,
связывающим совокупности действующих сил в
соответствующих геодинамических полях -
чем больше величины m и m*, тем больше
величины соответствующих сил.
Состав
рудных тел можно выразить следующим
образом: А*=
b/q (q - сумма SiO2, Al2O3, P2O5;
b-сумма остальных петрогенных, рудных и
летучих компонентов, что по смыслу
соответствует основности орудунения. Тогда
получаются уравнения регрессии,
связывающие относительную
дифференцированность магматитов с
генетически связанным оруденением
А*= l - sL
(10)
и силой
геодинамического поля
A*=((DA×F×t)/(DС×
r ×d×W))
- k
(11)
- l, s, r, d, k -
эмпирические коэффициенты.
Очевидно,
что основность руд, образованных в
результате магматической дифференциации,
прямо пропорциональна изменению
структурно-химического состояния
магматических пород, силе геодинамического
поля во времени и обратно пропорциональна
объему магматического очага и изменению
параметра С.
Из
приведенных соотношений следует важный
вывод. Тектоно-магматические системы
являются геодинамически подобными, если
имеют одинаковую скорость распространения
геодинамического поля (скорость
деформирования) и подобные размеры с
коэффициентом подобия р=10n;
геодинамически подобным тектоническим
структурам принадлежат магматические
образования с одинаковой относительной
дифференцированностью состава и
генетически связанным оруденением, с
соответствующими энергетическими
параметрами.
По результатам структурно-химического
моделирования и в соответствии с
развиваемыми представлениями, для
Джалиндинской тектоно-магматической
системы были рассчитаны значения L,
определены масштабы измерения структурно-химического
состояния (dA1,2,3)
на уровне отдельных структур, их элементов
и всей системы в целом, получены
характерные числа (квантовые числа) и
связывающие их зависимости (табл.1):
1Nkобщ = DAkобщ/dAобщ,
(12)
2Nk =
DAkобщ/dAk,
(13)
3Nk =
DAkстр/dAk,
(14)
где 1Nkобщ,
2Nk, 3Nk - соответственно 1,2,3 числа
уровня k, показывающие количество квантов
или количество элементарных ячеек,
характеризующих данный уровень; DAkобщ,
DAkстр
- соответственно, проекция изменения и
полное изменение структурно-химического
состояния на данном уровне; dAобщ,
dAk
- масштабы измерения (кванты) структурно-химического
состояния всей системы и отдельных ее
уровней.
Сумма чисел 1Nkобщ для
структурных элементов системы (Z и V
структуры) дает общее внутреннее число
системы 1Nобщ = 7. Для отдельных
элементов системы эти числа также
стремятся к целым значениям. Общее
внутреннее число (1Nобщ) системы и
общее число (1Nkобщ) элемента
системы связаны соотношением:
1Nkобщ = (3Nk/1Nобщ)pi,
(15)
где р=2.154....
Показатель степени i для Джалиндинской
системы принимает значения 0; 1; 2; 0.5; 0 в
последовательности от массива к комплексам
даек.
Общее число системы и внутреннее число
элемента системы может быть выражено как:
2Nk = (3Nk/1Ns(k)общ)r.
(16)
Здесь 1Ns(k)общ - общее
квантовое число системы; r - эмпирический
коэффициент, который принимает значения 1 (для
первого комплекса) и 2 - для всех остальных.
Графическое
моделирование действующих сил, в
соответствии с полученными аналитическими
выражениями, может осуществляться при
помощи конусов и фигур по своей симметрии
относящихся к одной из его подгрупп (пирамиды,
параболлоиды и др.), т.к. сила и
перичисленные фигуры относятся к одной
группе симметрии.
Неопределенности,
возникающие при квантово-геодинамическом
моделировании обусловлены, главным образом,
точностью определения пространственно-временных
границ структур и невозможностью учета в
модели на данный момент их трехмерности (см.
определение).
Приводимые
аналитические выражения отличаются тем,
что скорости деформирования,
пространственные размеры, состав
магматических пород и руд принимают
дискретные значения. Поэтому, с учетом
геодинамического подобия тектоно-магматических
систем, могут быть подобраны скорости
деформирования, удовлетворяющие различным
по длительности периодам развития систем, в
том числе и поцессам современного
гидротермального минералообразования.
Выполненная ранее (Тишкин, 1994; 1996; 1997)
проверка полученных уравнений на их
пригодность для определения параметров
геодинамического пространства в диапазоне
“планета Земля - физический эксперимент”,
показала результаты, хорошо сопоставимые с
геолого-геофизическими и
экспериментальными данными по
моделированию процессов
разломообразования в литосфере.
Результаты
моделирования
Джалиндинская
тектоно-магматическая система,
сформированная в позднеюрское-раннемеловое
время, локализуется в центральной части
Соловьевского свода (морфоструктуры
центрального типа), выделенного впервые при
дешифрировании космоснимков (Соловьев,1978;
Кулаков и др.,1983). Последующие специальные
геологические исследования и анализ
геолого-геофизических и
геоморфологических данных, а также
специальные полевые исследования,
подтвердили правомерность выделения
Соловьевского свода как долгоживущей,
предположительно с докембрия,
морфоструктуры центрального типа (Мясников
и др.,1984; Мясников, Залищак,1988).
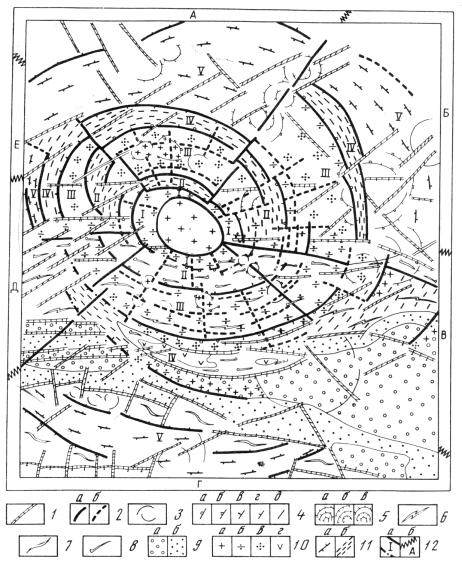
Соловьевский
свод (радиус R»40
км) расположен в пределах Амуро-Охотской
складчатой системы (рис.1), разделяющей
Алдано-Становой и Амурский геоблоки (Красный,1980
и др.) или, согласно представлениям М.Г.Золотова
и В.В.Соловьева, в области интерференции
Алданской (R»950
км) и Амурской (R»1200
км) мегаструктур центрального типа (см. рис.1).
В табл. 4 Соловьевский свод при n=2 и
Джалиндинская тектоно-магматическая
система имеют одинаковые геодинамические
параметры. Значение числа n>¦2¦ для
Соловьевского свода предполагает развитие
на площади этой структуры щелочных
магматитов, которые пока не обнаружены,
следовательно такой вариант интерпретации
отпадает. При n<¦2¦, время деформирования
Соловьевского свода оказывается
значительно меньше суммы времен
деформирования его элементов, т.е. этот
вариант также кажется не подходящим. Тогда
при n=¦2¦ площадь Соловьевского свода может
рассматриваться как площадь Джалиндинской
тектоно-магматической системы, но данные по
магматизму получены на площади первых двух
концентров по логике прежде должны
параллелизоваться с площадью структуры
третьего концентра S3=375 км2 (см.
табл. 2). Из этого можно предположить, что
структура Соловьевского свода S6 и
структура его внутренних элементов с
площадью S3, S0 в позднеюрское-раннемеловое
время были геодинамически подобны и имели
дальний порядок. Рассмотренные
пространственно-временные особенности, как
кажется, и отражают существо регионального
геодинамического контроля проявления
специфических черт магматизма и оруденения
в пределах локальных структур.
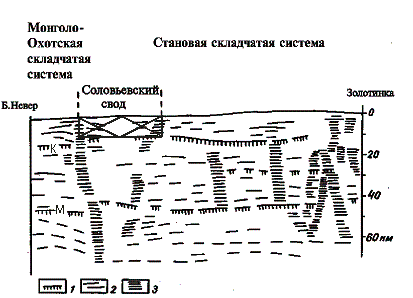
На рис. 3 изображена схема действующих
сил в разрезе Соловьевской структуры (как
закрытой системы; показаны структуры с
радиусами R6, R5, R4, R3, R0)
с предполагаемыми зонами разуплотнения для
уровней 6m6 и 3m6 (первая цифра - квантовый
уровень структуры верхнего иерархического
уровня, вторая цифра - внутренний квантовый
уровень рассматриваемой структуры). Здесь
же, на врезке, показано изменение скоростей
деформирования с глубиной для Соловьевской
структуры и зон разуплотнения
соответствующего уровня, а также изменение
скоростей деформирования структур
магматической колонны с определенными
типами структурно-химического состояния. И
кроме того, показаны вычисленные по
значениям соответствующих квантовых чисел,
границы (плоскости) областей магматической
колонны с данным типом структурно-химического
состояния и соответствующими типами рудной
минерализации. Суммируя результаты
моделирования, можно заключить следующее:
1) Зоны разуплотнения уровня 6m6
располагаются симметрично относительно
центра инверсии и имеют область
динамического равновесия, совпадающую (S5=80
км2) с областью структуры
соответствующего уровня. Зоны
разуплотнения уровня 3m6 (m*=-3) также
симметричны относительно центра инверсии
уровня 6m6, а кроме того, в каждой из своих
частей, имеют свои области динамического
равновесия (S5=8 км2).
2) Границы (плоскости) областей
магматической колонны с данным типом
структурно-химического состояния
приурочены к областям динамического
равновесия структур различных
иерархических уровней. Однако, учитывая
объемный характер границы, размеры
выделенных областей должны
рассматриваться как условные (ориентировочные).
3) Приведенные площади структур тектоно-магматической
системы вписываются в площади сечений зон
разуплотнений с радиусами R3 (Z тип), R0
(V тип) при S6=3750 км2, h6=9.84 км
и в площади сечений зон с радиусом R3 (Z
и V типы) при S6=375 км2, h6=4.57
км (зоны разуплотнения уровня 3m6 при m*=-3
отвечают последнему варианту). В первом
случае, следует заключить, что структура
"песочных часов" является следствием
сочетания структур двух смежных
структурных уровней 6m6 (Z тип) и 3m6 (V тип). Во
втором случае, мы имеем дело с одним
структурным уровнем, но с двумя структурами
типа "песочных часов". Положение
сохраняется и при изменении величины числа
n для структур V типа. Критерии, для принятия
решения в этом вопросе, отсутствуют.
Последнее обстоятельство, а также
отсутствие методики учета объемного
характера областей раздела, не позволило
привязать к глубинной структуре
вычисленные сечения тектоно-магматической
системы и рассчитать более точное
положение возможных областей
рудогенерации в модели - в настоящий момент
это возможно произвольно - методом подгонки.
4) Изменение скорости деформирования
структур и зон разуплотнения одного уровня
в разрезе происходят в противофазе: с
уменьшением скорости деформирования
структуры увеличивается скорость
деформирования зон разуплотнения. Это
может объясняться характером изменения
величины сил F1 и F2 в структуре и
зонах разуплотнения. Графики скорости
деформирования структур тектоно-магматической
системы с данным типом структурно-химического
состояния, положение которых задавалось
проекцией на пограничную плоскость, в
отдельных участках конформны графикам для
зон разуплотнения и соответствующей
структуры. В целом, скорость деформирования
структур различной иерархии на одном
гипсометрическом уровне изменяется
нелинейно и имеет сложный полимодальный
характер. Это, в свою очередь, должно
обусловливать, нелинейность
тектонического, магматического и
рудообразующего процессов в пространстве и
времени, что, в частности, подтверждается
для магматических образований на примере
изменения относительной
дифференцированности их состава в
зависимости от глубины локализации
соответствующей области тектоно-магматической
системы. Вместе с тем, подобие размеров
сечений магматической колонны и
тектонической структуры Соловьевского
свода не исключает проявления и их
геодинамического подобия, т.е.
существования нелокальной симметрии (дальнего
порядка).

5) Полученные значения времени
накопления упругих, вязких и хрупких
напряжений по скоростям деформирования
структур Джалиндинской тектоно-магматической
системы оказываются сопоставимыми с
оценками времен формирования рудных
районов, полей и месторождений (Старостин,
1993), и по этому признаку, рассматриваемая
система относится к объектам,
формировавшимся в условиях
высокоскоростного режима. По структурным
парагенезисам же этот объект следует
отнести к повышенно скоростным.
По оценкам времен кристаллизации
пластиновидных интрузий базитового
состава мощностью 5 км на глубине 5-10 км ее
температура за 0.5 млн. лет изменится от 1300 до
7500С (Шарапов, Черепанов, 1986). По биотит-амфиболовому
термометру для Джалиндинского массива,
размеры и время формирования которого
значительно меньше принятых в расчетах,
фиксируются значения температур в пределах
700-8000С. Из этого следует, что время
кристаллизации магматического расплава
сопоставимо со временем формирования
магматической камеры (временем накопления
деформаций), и, следовательно, для момента
кристаллизации и продолжающейся
дифференциация магмы скорости
деформирования магмовмещающей структуры
оказываются сопоставимыми.
Заключение
Аналитические зависимости, связывающие
состав и относительную
дифференцированность состава
магматических образований и оруденения с
вертикальными и горизонтальными размерами
тектонических образований и скоростями их
деформирования, содержат в своей структуре
коэффициенты подобия, группирующиеся в
систему, что позволяет применять
соответствующие аналитические выражения
для геологических объектов различной
иерархии, а также при физическом
моделировании геодинамических процессов.
Полученные аналитические выражения также
отличаются тем, что скорости
деформирования, пространственные размеры,
состав магматических пород и руд принимают
дискретные значения. Поэтому, с учетом
геодинамического подобия тектоно-магматических
систем, могут быть подобраны скорости
деформирования, характерные для процессов
различной длительности, в том числе и для
систем современного гидротермального
минералообразования.
ЛИТЕРАТУРА
1.
Гуров Л.П.
Минеральные ассоциации Кировского
золоторудного месторождения (Верхнее
Приамурье)//Золотая минерализация Верхнего
и Среднего Приамурья. Владивосток: ДВНЦ
ДВГИ АН СССР. 1978. С.11-86.
2.
Красный Л.И.
Глобальная система геоблоков. М: Недра. 1984.
224 с.
3.
Кулаков А.П.,
Сорокин А.П., Мясников Е.А. Новые данные о
морфоструктуре восточной окраины зоны БАМ (по
материалам космических съемок) //
Морфоструктурные исследования на Дальнем
Востоке. Владивосток: ДВНЦ АН СССР. 1983. С.48-61.
4.
Мясников Е.А.,
Залищак Б.Л. Исследования морфоструктур
центрального типа в прогнозно-металлогенических
целях (Верхнее Приамурье) //
Морфотектонические системы центрального
типа Сибири и Дальнего Востока. М.:Наука. 1988.
С.184-190.
5.
Мясников Е.А.,
Кулаков А.П., Залищак Б.Л. Морфоструктуры
центрального типа Верхнего Приамурья.//Морфоструктуры
центрального типа Дальнего Востока.
Владивосток: ДВНЦ АН СССР. 1984. С.39-52.
6.
Соловьев В.В.
Структуры центрального типа территории
СССР по данным геолого-геоморфологического
анализа:(объясн. зап. к карте морфоструктур
центр.типа). Л.: ВСЕГЕИ. 1978. 110 с.
7.
Старостин В.И.
Скорости формирования геологических
структур и рудообразование // Отеч. геол.,1993.
№ 7. С.31-40.
8.
Тишкин Б.М.,
Пахомова В.А. К использованию результатов
термобарометрии при интерпретации
зональности оруденения на плутоногенном
месторождении золота // Глубинность
распространения и элементы зональности
эндогенной минерализации Дальнего Востока.
Владивосток: ДВО ДВГИ АН СССР. 1987. С.86-99.
9.
Тишкин Б.М.
Квантовая геодинамика - новая парадигма в
геологии // Вестник ДВО РАН. 1994. № 4. С.91-102.
10.
Тишкин Б.М. Связь
геодинамических параметров тектонических
структур с составом эндогенного вещества //
Тихоок. геолог., 1996. Т.!5. № 1. С.67-79.
11.
Тишкин Б.М.
Геодинамическое подобие тектоно-магматических
систем. / Автореф. дисс. ... канд. геолог.-мин.
наук Хабаровск. 1997. 30 с.
12.
Шарапов В.Н.,Черепанов
А.Н. Динамика дифференциации магм.
Новосибирск: 1986. Тр.ИгиГ. вып.642. 188 с.
13
. Щеглов
А.Д. Основные проблемы
современной металлогении. Л.: Недра, 1987. 231 с.