В.К. Булгаков, Н.В. Булгаков
Хабаровский государственный технический университет, nboulgakov@mail.ru
Аннотация. В статье приводится анализ семейства разностных схем численного расчета двумерных отрывных турбулентных течений и теплопереноса.
Сначала рассмотрим разностные схемы метода контрольного объёма (МКО) [1] на примере одномерной стационарной задачи конвекции и диффузии, а затем полученные результаты используем при построении разностных схем МКО для двумерных турбулентных течений и теплообмена.
1. Исследование разностных схем МКО на примере одномерной задачи конвекции и диффузии
Конвекция и градиентный перенос (диффузия) в сплошной среде скалярной величины, например, температуры, описывается законом сохранения рассматриваемой величины и уравнением неразрывности, которые для одномерного случая и отсутствия объемного теплового источника имеют вид:
![]() (1)
(1)
![]() (2)
(2)
где
![]() – плотность и
скорость одномерного движения сплошной
среды;
– плотность и
скорость одномерного движения сплошной
среды;
![]() – коэффициент градиентного переноса
рассматриваемой величины
– коэффициент градиентного переноса
рассматриваемой величины
![]() .
.
![]() – суммарный поток
величины
– суммарный поток
величины
![]() , обусловленный конвекцией и градиентным
переносом.
, обусловленный конвекцией и градиентным
переносом.
Из уравнения (2) следует, что
![]() .
.
Рассмотрим область
![]() и случай
и случай
![]() . Тогда уравнение (1) можно записать в виде:
. Тогда уравнение (1) можно записать в виде:
![]() (3)
(3)
Рассмотрим для уравнения (1.3) краевые условия I рода:
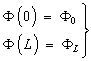 (4)
(4)
В переменных
![]()
![]() краевая задача
(3, 4) имеет вид:
краевая задача
(3, 4) имеет вид:
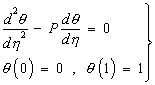 (5)
(5)
где
![]() – параметр задачи,
называемый числом Пекле.
– параметр задачи,
называемый числом Пекле.
Краевая задача (5) имеет решение:
![]()
или в переменных
![]() имеем:
имеем:
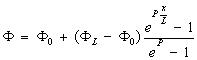 (6)
(6)
Рассмотрим
на отрезке
![]() разностную сетку
разностную сетку
![]() , часть которой показана на рис. 1.
, часть которой показана на рис. 1.
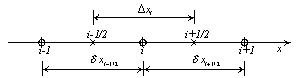
Рис.1.
Схема одномерной разностной сетки на
отрезке
![]()
В узлах
![]() определена
сеточная функция
определена
сеточная функция
![]() , а узлы
, а узлы
![]() находятся на
гранях контрольного объема, содержащего
узел
находятся на
гранях контрольного объема, содержащего
узел
![]() . Проинтегрируем уравнение (1) по
контрольному объему
. Проинтегрируем уравнение (1) по
контрольному объему
![]() , в
результате получим:
, в
результате получим:
![]() (7)
(7)
Используем
точное решение (6) рассматриваемой краевой
задачи в качестве профиля между узлами
сетки
![]() для вычисления
потоков
для вычисления
потоков
![]() на гранях
контрольного объема
на гранях
контрольного объема
![]() .
.
На отрезке
![]() имеем:
имеем:
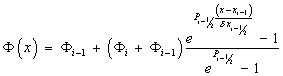
где
![]() –
сеточное число Пекле.
–
сеточное число Пекле.
На
отрезке
![]() соответственно
имеем:
соответственно
имеем:
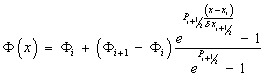 ,
где
,
где
![]() –
сеточное число Пекле.
–
сеточное число Пекле.
Откуда для
потоков через грани
![]() контрольного
объема можем записать:
контрольного
объема можем записать:
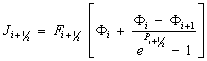 (8)
(8)
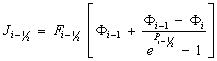 (9)
(9)
Наряду
с величиной
![]() , характеризующей интенсивность конвекции,
введем еще
, характеризующей интенсивность конвекции,
введем еще
![]() , являющуюся диффузионной проводимостью.
Тогда на равномерной сетке сеточное число
Пекле
, являющуюся диффузионной проводимостью.
Тогда на равномерной сетке сеточное число
Пекле
![]() .
.
Подставляя полученные выражения для потоков через грани контрольного объема в уравнение (7) имеем:
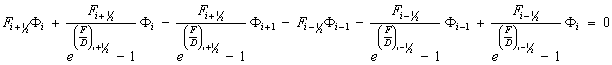
или введя коэффициенты разностной схемы:
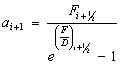 (10)
(10)
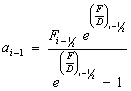 (11)
(11)
![]() (12)
(12)
получим так называемую экспоненциальную разностную схему [1] :
![]() (13)
(13)
Следует отметить, что при выполнении уравнения неразрывности (2) коэффициент
![]() (12´)
(12´)
Из
построения разностной схемы (использование
в качестве профилей между узлами сетки
точного решения (6)) очевидно, что для
одномерной стационарной задачи и
![]() экспоненциальная
схема будет давать точное решение для
любого значения сеточного числа Пекле
экспоненциальная
схема будет давать точное решение для
любого значения сеточного числа Пекле
![]() и при любом числе
узлов разностной сетки.
и при любом числе
узлов разностной сетки.
Продолжим анализ формул для потоков через грани контрольного объема.
Исходя
из выражений (8, 9), учитывая, что
![]() и введя
зависимости:
и введя
зависимости:
![]() (14)
(14)
![]() (15)
(15)
можем записать:
![]() (16)
(16)
![]() (17)
(17)
Зависимости (14, 15) обладают следующими свойствами.
![]() ,
,
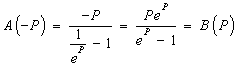 ,
,
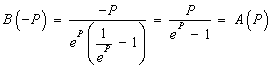
Зависимость
![]() при
при
![]() имеет
горизонтальную асимптоту – ось
имеет
горизонтальную асимптоту – ось
![]() , при
, при
![]() наклонную
асимптоту
наклонную
асимптоту
![]() . Зависимость
. Зависимость
![]() является
зеркальным отражением зависимости
является
зеркальным отражением зависимости
![]() относительно оси
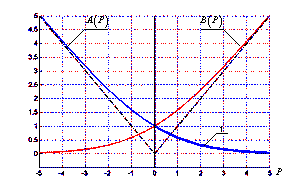
абсцисс. Характер зависимостей
относительно оси
абсцисс. Характер зависимостей
![]() показан на рис. 2.
показан на рис. 2.
Из
выписанных свойств зависимостей
![]() имеем для
имеем для
![]() :
:
![]()
Для
![]() очевидно имеем:
очевидно имеем:
![]() . Поэтому для
. Поэтому для
![]() можем записать:
можем записать:
![]() (18)
(18)
где оператором
![]() обозначен
обозначен
![]() .
.
Аналогично
при
![]() имеем:
имеем:
![]() (19)
(19)
Отметим,
что в дальнейшем, если не будет оговорено,
под числом
![]() будем понимать
сеточное число Пекле
будем понимать
сеточное число Пекле
![]() .
.
Формулы
(18, 19) позволяют описать функции
![]() при
при
![]() функцией
функцией
![]() определенной
только на интервале
определенной
только на интервале
![]() , т.е. для положительных значений
, т.е. для положительных значений
![]() (кривой 1 рис. 2).
Патанкаром предложена следующая степенная
аппроксимация кривой 1 (зависимости
(кривой 1 рис. 2).
Патанкаром предложена следующая степенная
аппроксимация кривой 1 (зависимости
![]() ):
):
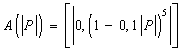 (20)
(20)
На рис. 3 в более
крупном масштабе представлена посчитанная
по формуле (14) зависимость
![]() – кривая 1, здесь же
кривой 2 показана зависимость (20). Как видно
из рисунка зависимость (20) хорошо
аппроксимирует исходную зависимость (14).
– кривая 1, здесь же
кривой 2 показана зависимость (20). Как видно
из рисунка зависимость (20) хорошо
аппроксимирует исходную зависимость (14).
Недостатком
формулы (20) является то обстоятельство, что
для расчета каждого значения
![]() требуется
выполнение 5 операций. В тоже время очевидно,
что аппроксимация (20) является не
единственно возможной.
требуется
выполнение 5 операций. В тоже время очевидно,
что аппроксимация (20) является не
единственно возможной.
Простейший вариант аппроксимации формулы (14) может быть следующий:
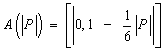 (21)
(21)
На рис. 3 кривой 3 показана зависимость (21).
Можно рассмотреть семейство разностных схем, основанных на зависимостях:
![]() (22)
(22)
где
![]() , а
, а
![]() подбирается для
каждого
подбирается для
каждого
![]() .
.
В частности, на рис. 3 кривой 4, представлена зависимость :
![]() (23)
(23)
Представляет интерес показательная зависимость
![]() (24)
(24)
На рис. 3 она представлена кривой 5.
Как следует из сравнения кривых 1, 4, предложенная зависимость (23) неплохо аппроксимирует формулу (14) и может быть использована для построения более экономичной разностной схемы.
Вернемся
к разностной схеме (13). Продолжим
рассмотрение случая равномерной сетки (
![]() ), коэффициент диффузии
), коэффициент диффузии
![]() , выполняется уравнение неразрывности (
, выполняется уравнение неразрывности (
![]() ). Тогда для коэффициентов разностной схемы
(10, 11, 12´) имеем:
). Тогда для коэффициентов разностной схемы
(10, 11, 12´) имеем:
![]() ,
,
![]()
![]()
![]()
А разностную схему (13) можно записать в форме:
![]() (25)
(25)
где коэффициенты:
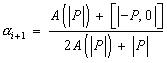 (26)
(26)
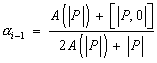 (27)
(27)
зависят только от
сеточного числа Пекле
![]() .
.
Для
анализа различных разностных схем МКО (в
основу которых положены различные
рассмотренные выше зависимости
![]() ) рассмотрим результаты расчетов
коэффициентов
) рассмотрим результаты расчетов
коэффициентов
![]() , которые являются весовыми коэффициентами.
, которые являются весовыми коэффициентами.
На рис. 4 кривыми 1 представлены результаты расчета для экспоненциальной схемы, т.е. для
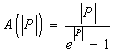 (28)
(28)
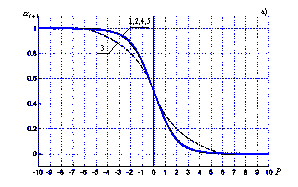
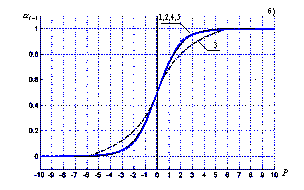
Кривые 2 соответствуют схеме со степенным законом (20), кривые 3 для схемы с линейным законом (21), кривые 4 для схемы с законом (23), кривые 5 для схемы с показательным законом (24). Как следует из сравнения кривых 2-5 с кривыми 1 даже простая схема с линейным законом (21) дает физически реальные результаты.
На рис 5 показаны расхождения коэффициентов разностной схемы (25) посчитанные для экспоненциальной схемы (28) и для законов (20, 21, 23, 24), аппроксимирующих экспоненциальную схему. Кривая 1 – соответствует закону (20), кривая 2 –закону (23), 3 –закону (24), 4 – линейному закону (21).
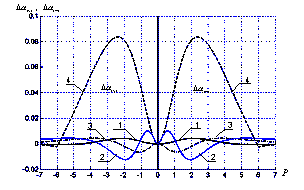
Рис.5. Распределение дисперсии коэффициентов разностной схемы от параметра Р.
Максимальное отклонение коэффициентов
![]() и
и
![]() для схемы с
линейным законом (21), от соответствующих
коэффициентов экспоненциальной схемы
менее 9% (при
для схемы с
линейным законом (21), от соответствующих
коэффициентов экспоненциальной схемы
менее 9% (при
![]() ). Схемы с законом (23) и показательным
законом (24) практически не уступают схеме со
степенным законом (20) Патанкара.
). Схемы с законом (23) и показательным
законом (24) практически не уступают схеме со
степенным законом (20) Патанкара.
Для
сравнения рассмотренного семейства
одномерных схем МКО рассмотрим результаты
численного решения модельной краевой
задачи (3-4), имеющей аналитическое решение
(6), используя разностные схемы (28, 20, 21, 22´,
24) при различных числах Пекле задачи
![]() . Для всех схем использовалась равномерная
сетка с шагом
. Для всех схем использовалась равномерная
сетка с шагом
![]() , так что
сеточное число Пекле
, так что
сеточное число Пекле
![]() .
.
В табл. 1
представлены результаты расчетов для
сеточного числа Пекле
![]()
Результаты расчётов погрешностей для сеточного числа Пекле (Рs= -5) Таблица. 1
|
x |
Рассчитанные зависимости |
||||
|
(6) |
(20) |
(23) |
(24) |
(21) |
|
|
0.00 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
|
0.05 |
1.2227 |
1.2227 |
1.2184 |
1.2235 |
1.2196 |
|
0.10 |
1.3961 |
1.3961 |
1.3895 |
1.3974 |
1.3914 |
|
0.15 |
1.5312 |
1.5312 |
1.5235 |
1.5327 |
1.5257 |
|
0.20 |
1.6364 |
1.6364 |
1.6285 |
1.6379 |
1.6307 |
|
0.25 |
1.7183 |
1.7183 |
1.7106 |
1.7198 |
1.7128 |
|
0.30 |
1.7821 |
1.7821 |
1.7750 |
1.7835 |
1.7771 |
|
0.35 |
1.8318 |
1.8318 |
1.8254 |
1.8331 |
1.8273 |
|
0.40 |
1.8705 |
1.8705 |
1.8649 |
1.8716 |
1.8665 |
|
0.45 |
1.9007 |
1.9007 |
1.8959 |
1.9016 |
1.8972 |
|
0.50 |
1.9241 |
1.9241 |
1.9201 |
1.9249 |
1.9213 |
|
0.60 |
1.9567 |
1.9567 |
1.9539 |
1.9572 |
1.9547 |
|
0.70 |
1.9764 |
1.9764 |
1.9747 |
1.9767 |
1.9752 |
|
0.75 |
1.9831 |
1.9831 |
1.9818 |
1.9833 |
1.9822 |
|
0.80 |
1.9883 |
1.9883 |
1.9874 |
1.9885 |
1.9877 |
|
0.85 |
1.9924 |
1.9924 |
1.9918 |
1.9925 |
1.9920 |
|
0.90 |
1.9956 |
1.9956 |
1.9952 |
1.9957 |
1.9953 |
|
0.95 |
1.9981 |
1.9981 |
1.9979 |
1.9981 |
1.9979 |
|
1.00 |
2.0000 |
2.0000 |
2.0000 |
2.0000 |
2.0000 |
|
DL2E |
8.2e-05 |
0.04669 |
0.00899 |
0.03333 |
|
|
RMS |
8.2e-06 |
0.00464 |
0.00089 |
0.00331 |
|
|
RDE |
4.5e-06 |
0.00255 |
0.00049 |
0.00182 |
|
|
Время счета |
1 |
0.96733 |
1.00896 |
0.97639 |
|
Для
количественной оценки погрешности решений
разностных задач (20, 23, 24, 21) по сравнению с
точным решением (6) воспользуемся
дискретной
![]() - погрешностью [4]:
- погрешностью [4]:
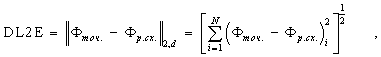
среднеквадратической ошибкой [5]:
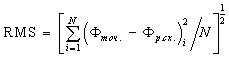
и относительной
![]() - погрешностью [6]:
- погрешностью [6]:
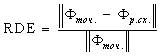 ,
где
,
где
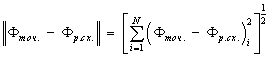 ,
,
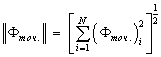
Погрешности
DL2E,
RMS, RDE
при
![]() показаны в табл. 1.
Здесь же представлено время
счета задачи по рассматриваемым
разностным схемам. В табл. 2 представлены
аналогичные результаты расчетов для
сеточного числа Пекле
показаны в табл. 1.
Здесь же представлено время
счета задачи по рассматриваемым
разностным схемам. В табл. 2 представлены
аналогичные результаты расчетов для
сеточного числа Пекле
![]() .
.
Результаты расчётов погрешностей для сеточного числа Пекле (Рs= 10) Таблица 2
|
x |
Рассчитанные зависимости |
||||
|
(6) |
(20) |
(23) |
(24) |
(21) |
|
|
0.00 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
|
0.05 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
|
0.10 |
1.0001 |
1.0001 |
1.0001 |
1.0001 |
1.0001 |
|
0.15 |
1.0002 |
1.0002 |
1.0002 |
1.0001 |
1.0002 |
|
0.20 |
1.0003 |
1.0003 |
1.0004 |
1.0003 |
1.0004 |
|
0.25 |
1.0005 |
1.0005 |
1.0007 |
1.0005 |
1.0006 |
|
0.30 |
1.0009 |
1.0009 |
1.0011 |
1.0008 |
1.0011 |
|
0.35 |
1.0015 |
1.0015 |
1.0019 |
1.0014 |
1.0018 |
|
0.40 |
1.0024 |
1.0024 |
1.0031 |
1.0023 |
1.0029 |
|
0.45 |
1.0040 |
1.0040 |
1.0050 |
1.0039 |
1.0048 |
|
0.50 |
1.0067 |
1.0067 |
1.0082 |
1.0064 |
1.0078 |
|
0.60 |
1.0183 |
1.0183 |
1.0215 |
1.0177 |
1.0207 |
|
0.70 |
1.0497 |
1.0498 |
1.0562 |
1.0485 |
1.0547 |
|
0.75 |
1.0820 |
1.0821 |
1.0908 |
1.0803 |
1.0888 |
|
0.80 |
1.1353 |
1.1353 |
1.1468 |
1.1330 |
1.1441 |
|
0.85 |
1.2231 |
1.2231 |
1.2372 |
1.2203 |
1.2339 |
|
0.90 |
1.3679 |
1.3679 |
1.3832 |
1.3648 |
1.3796 |
|
0.95 |
1.6065 |
1.6066 |
1.6190 |
1.6040 |
1.6161 |
|
1.00 |
2.0000 |
2.0000 |
2.0000 |
2.0000 |
2.0000 |
|
DL2E |
24.7e-05 |
0.0664 |
0.01325 |
0.05093 |
|
|
RMS |
2.46e-05 |
0.00661 |
0.00131 |
0.00506 |
|
|
RDE |
2.19e-05 |
0.00588 |
0.00117 |
0.00451 |
|
|
Время счета |
1 |
0.97199 |
1.02979 |
0.99988 |
|
Как следует из анализа таблиц 1,2, все разностные схемы (20-24) дают хорошую точность решения, с точки зрения затрат компьютерного времени вне конкуренции находится схема (23). Поэтому если рассматривать схемы как многократно используемый элемент решения более сложных задач (см. раздел 2, [3]), то схема (23) является более предпочтительной.
Отметим,
что для
![]() погрешности схем
(20-24) DL2E, RMS, RDE
между собой сближаются, что подтверждает
табл. 3, в которой представлены указанные
погрешности при
погрешности схем
(20-24) DL2E, RMS, RDE
между собой сближаются, что подтверждает
табл. 3, в которой представлены указанные
погрешности при
![]()
Результаты расчётов погрешностей для сеточного числа Пекле (Рs= -80; Рs= 80) Таблица 3
DL2E |
|
0.003669 |
0.026873 |
0.017824 |
0.1175 |
|
|
|||||
|
RMS |
|
0.000365 |
0.002674 |
0.001773 |
0.0116 |
|
|
|||||
|
RDE |
|
0.000183 |
0.001347 |
0.000893 |
0.00589 |
|
|
0.000356 |
0.002611 |
0.001732 |
0.01141 |
В
заключении этого раздела, используя
формулы (18, 19), запишем выражения для членов
![]() (16, 17) в следующей
форме:
(16, 17) в следующей
форме:
![]() (29)
(29)
![]() (30)
(30)
где
![]() ,
,
![]()
Формулы (29, 30), точнее их обобщение на двумерный случай будут использованы ниже при записи разностных уравнений МКО для двумерных задач.
2. Разностные уравнения МКО для двумерных задач
Рассмотрим
обобщенное уравнение переноса для
осредненного поля течения и модели
турбулентности
![]() и уравнение
неразрывности в форме [2]:
и уравнение
неразрывности в форме [2]:
![]() (31)
(31)
![]() (32)
(32)
Введем
разностную сетку
![]() , часть которой показана на рис. 7. На этом
рисунке показан контрольный объем,
содержащий узел
, часть которой показана на рис. 7. На этом
рисунке показан контрольный объем,
содержащий узел
![]() .
.
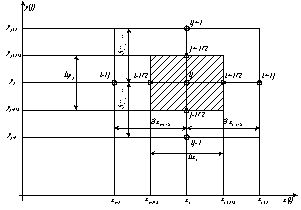
Рис. 6. Схема двумерной разностной сетки.
Проинтегрируем уравнения
(31, 32) по контрольному объему
![]() , где
, где
![]() .
.
В результате интегрирования уравнения (31) по контрольному объему получаем:
![]() (33)
(33)
Аналогично интегрируя уравнение неразрывности, имеем:
![]() (34)
(34)
где
![]() -
массовые расходы потока через грани
контрольного объема, т.е.
-
массовые расходы потока через грани
контрольного объема, т.е.
![]() ,
,
![]()
Учитывая,
что
![]() , из (33, 34) можем
записать:
, из (33, 34) можем
записать:
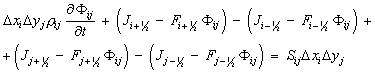 (35)
(35)
При
аппроксимации выражений в скобках
воспользуемся формулами (29, 30), полученными
при рассмотрении одномерной задачи, сделав
физически естественное допущение, что
двумерное течение через элементарный
контрольный объем
![]() представимо в виде
суперпозиции двух одномерных течений вдоль
представимо в виде
суперпозиции двух одномерных течений вдоль
![]() и вдоль
и вдоль
![]() . Тогда можем записать:
. Тогда можем записать:
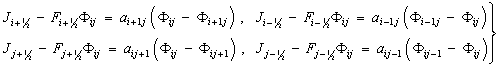 (36)
(36)
где
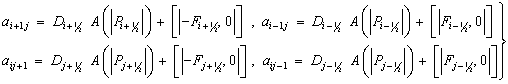 (37)
(37)
Здесь
![]() содержат площади
содержат площади
![]() соответствующих
граней:
соответствующих
граней:
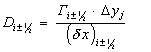 ,
,
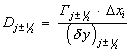 (38)
(38)
Коэффициенты
градиентного переноса на гранях
контрольного объема будем вычислять как
среднегеометрическое по значениям в
соседних узлах разностной сетки
![]() :
:
![]()
Для
чисел Пекле
![]() имеем по
определению:
имеем по
определению:
![]() (39)
(39)
Аппроксимируя
![]() , входящее в первое слагаемое уравнения (35)
разностным соотношением:
, входящее в первое слагаемое уравнения (35)
разностным соотношением:
![]() , где
, где
![]() значения на
предыдущем шаге по времени, а
значения на
предыдущем шаге по времени, а
![]() и все другие
слагаемые уравнения (35) на новом
и все другие
слагаемые уравнения (35) на новом
![]() - м слое, уравнение (35) можно записать в виде
следующего разностного:
- м слое, уравнение (35) можно записать в виде
следующего разностного:
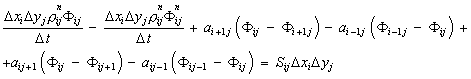 (40)
(40)
Для
случая, когда источниковый член
![]() зависит от
искомого решения, если возможно следует
провести его линеаризацию, точнее
аппроксимацию линейной функцией:
зависит от
искомого решения, если возможно следует
провести его линеаризацию, точнее
аппроксимацию линейной функцией:
![]()
где
![]() – “постоянная”
составляющая
– “постоянная”
составляющая
![]() , а
, а
![]() - коэффициент
линеаризации, они могут зависеть от решения
- коэффициент
линеаризации, они могут зависеть от решения
![]() и в этом случае
должны пересчитываться в процессе
итерационного цикла решения разностных
уравнений. Как показал Патанкар для
устойчивого счета необходимо, чтобы
и в этом случае
должны пересчитываться в процессе
итерационного цикла решения разностных
уравнений. Как показал Патанкар для
устойчивого счета необходимо, чтобы
![]() .
.
Разностное уравнение (40) можно записать в следующей окончательной форме:
![]() (41)
(41)
где
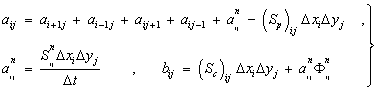 (42)
(42)
Полный алгоритм расчета и результаты численных исследований турбулентных двумерных отрывных течений, теплообмена и трения в ДВС подробно изложены в работе авторов [3].
Выводы
Проведен анализ семейства разностных схем численного расчета двумерных отрывных течений и теплопереноса. На первом этапе исследований рассмотрены разностные схемы метода контрольного объема на примере одномерной стационарной задачи конвекции и диффузии, затем, полученные результаты использованы при построении разностных схем метода контрольного объема для двумерных турбулентных течений и теплообмена. Предложенные схемы могут быть использованы для численного расчета тепломассопереноса в химических реакторах, двигателях внутреннего сгорания, парогенераторах и т.д.
ЛИТЕРАТУРА
1. Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. Пер. с англ. М.: Энергоатомиздат, 1984. 152 с.
2. Булгаков В.К., Булгаков Н.В., Галат А.А. Численное исследование турбулентных двумерных отрывных течений в двигателях внутреннего сгорания. Фундаментальные и прикладные вопросы механики: Сборник докладов международной научной конференции / Под ред. К.А. Чехонина. Хабаровск: Изд-во Хабар. гос. техн. университета, 2003. Т. 1 С. 50-61.
3. Булгаков В.К., Булгаков Н.В., Галат А.А. Метод расчета и численные исследования турбулентных двумерных отрывных течений в двигателях внутреннего сгорания. Препринт № 74 Вычислительного центра ДВО РАН. 2004. 48 с.
4. Флетчер К. Численные методы на основе метода Галеркина: Пер. с англ. М.: Мир, 1988. С.16
5. Флетчер К. Вычислительные методы в динамике жидкостей. Т1. Пер. с англ. – М.: Мир, 1991. С. 98.
6. Треногин В.А. Функциональный анализ. М.: Наука, 1980. С. 236-237.